Authors: Denis Kolegov (Matter Labs), Igor Konnov

After our success in specification and model checking of the ChonkyBFT consensus in Quint, we have decided to apply Quint and its tools to a slightly different domain: governance contracts in Solidity. This blogpost summarizes our experience and highlights the important modeling decisions we made.

1. Introduction

ZKsync Governance is a protocol that allows governance bodies (members), such as the ZKsync Security Council and Guardians, to manage ZKsync through regular and emergency procedures. The ZK token serves as the governance token for voting. The ZKsync Governance Procedures are maintained by the ZKsync Association and are updated to reflect any changes to the underlying smart contracts and on-chain mechanisms. They are intended as a high-level overview rather than a comprehensive guide.

The ZKsync governance smart contracts have been previously tried by well-known researchers in the field, who reported several vulnerabilities. When writing the formal specification, one of our goals was to see whether we could triage some of these reports and reproduce the vulnerabilities with the model checker. Another goal was to use the legal documents (especially devoted to the emergency response procedures) to ensure formally defined coverage of the contracts with state invariants.

As a result of our work, we have developed a protocol specification in Quint and over 50 invariants. All of them were tried with the randomized simulator of Quint as well as with the symbolic model checker Apalache. While we do not claim to have achieved a 100% accuracy in verifying these state invariants, since we were doing bounded model checking and randomized symbolic execution, we believe that the specification and model checking activity were quite valuable, for the following reasons:

  1. While writing the Quint specification, we have identified a few fragments of the Solidity code that could be improved, though they were not directly exploitable.

  2. While writing the state invariants and discussing them with the parties involved, we raised questions about the properties that led to further improvement of the freezability logic.

  3. We have reproduced several of the reported scenarios with the model checker and, for some of the scenarios, we showed that they were not reproducible in our specification.

  4. We have found that the legal documents of ZKsync governance were “verification-friendly”. It was relatively easy to translate many clauses from those documents into state invariants.

In this blogpost, we highlight the non-trivial parts of our specification process using Quint, overcoming challenges such as the lack of built-in primitives for Solidity and EVM. We created reference models for critical contract mechanisms, including multi-sig operations, cryptographic signatures, and EVM calls, and validated these models through symbolic model checking with SMT solvers.

2. Overview of the ZKsync Governance Protocol

The ZKsync Governance Protocol is structured around a governance system with four distinct voting classes:

  • Token Assembly: Comprised of ZK tokenholders, who delegate the voting power of ZK tokens they hold to ZKsync addresses in order to (indirectly) participate in the ZKsync governance system.

  • ZK Foundation: A privileged supporting entity.

  • Guardians: A group of 5 to 8 actors with administrative privileges.

  • Security Council: A group of 9 to 12 actors with administrative privileges.

The key characteristics of this governance system include:

  • Any proposal from the Token Assembly requires approval from either the Guardians or the Security Council to proceed.

  • In collaboration, the ZK Foundation, Guardians, and Security Council can initiate an emergency upgrade.

  • The Security Council can freeze the ZKsync protocol in case of an emergency.

  • Guardians have the independent power to veto proposals.

In our research, we have modeled the L1 contracts in Solidity that can be found in the following GitHub repository. We give a brief overview of the contracts below.

Multisig. The Multisig contract is an abstract implementation of a multi-sig wallet, allowing a group of governance bodies to authorize actions collectively by meeting a predefined signature threshold. It uses EIP-1271 for secure signature verification, requiring signatures from unique members in a sorted order. The contract ensures that the number of signatures meets or exceeds the required threshold before validating them against the list of authorized members. If the signatures are valid, the action is authorized, enabling secure collective decision-making within a decentralized environment.

Security Council. The SecurityCouncil contract responsible for communication with the security experts of the ZKsync protocol. It operates as a multi-sig wallet with 12 members and handles critical functions such as approving protocol upgrades, initiating protocol freezes, and unfreezing the protocol when necessary.

Key Functions:

  • Upgrade Approval: Requires 6 signatures to approve protocol upgrades, ensuring consensus among security experts.

  • Soft Freeze: Initiated by a smaller threshold of council members (default of 3 signatures), temporarily halting protocol changes.

  • Hard Freeze: 9 signatures are required to trigger a full protocol freeze.

  • Unfreeze: It also requires 9 signatures to unfreeze, resuming normal protocol operations.

  • Threshold Management: The council can adjust the soft freeze threshold, with changes requiring 9 signatures and expiring after a set period.

Each function call is secured using EIP-712 signatures, ensuring only authorized members can initiate critical security functions.

Guardians. The Guardians contract safeguards the ZKsync protocol, providing essential governance functions such as approving upgrades, managing L2 proposals, and extending legal veto periods. This contract also uses a multi-signature mechanism, requiring a specific number of guardian approvals for different actions.

Key functions include:

  • Upgrade Approval: Guardians can approve protocol upgrades with 5 signatures, ensuring a consensus-driven approach to critical changes.

  • Legal Veto Extension: Guardians can extend the legal veto period for L1 upgrade proposals with just 2 signatures, adding a layer of security.

  • L2 Proposal Management: Guardians can propose and cancel L2 governance proposals, requiring 5 signatures. The contract uses EIP-712 for secure and verifiable signature handling, preventing unauthorized actions. Each proposal or veto action is recorded with a unique nonce to protect against replay attacks, ensuring that every decision is unique and intentional.

Emergency Upgrade Board. The EmergencyUpgradeBoard contract facilitates emergency protocol upgrades through a coordinated process involving three critical entities: the Security Council, Guardians, and the ZK Foundation. Each entity must provide multi-sig approval for any emergency upgrade to proceed, ensuring consensus among key stakeholders. The contract leverages EIP-712 for secure and verifiable signature handling, defining specific type hashes for each group’s approval process. Upon receiving the necessary signatures, the contract validates them against the specified type hashes. If all approvals are verified, the contract delegates the upgrade execution to the ProtocolUpgradeHandler.

Protocol Upgrade Handler. The ProtocolUpgradeHandler is a backend contract that manages the upgrade process for the ZKsync protocol. It holds ownership of all ZKsync contracts on both L1 and L2, ensuring that upgrades follow a secure and structured process. The contract also manages emergency actions, such as protocol freezes and self-upgrades.The upgrade process involves several stages: proposal, legal veto, approval, pending, and execution:

  • Proposal: Delegates propose a protocol upgrade by sending a special message initiating the upgrade process.

  • Legal Veto Period: Guardians can veto the upgrade within a 3-day period, extendable to 7 days.

  • Approval: Requires approval from the Security Council or Guardians. The Security Council can approve immediately, while Guardians’ approval requires a 30-day waiting period.

  • Pending: A mandatory delay before execution allows for final preparations.

  • Execution: The approved changes are executed, completing the upgrade process.

3. Modeling the Protocol

We used Quint to produce an executable specification of the ZKsync Governance contracts, which are written in Solidity, and wrote several basic tests to check that the specification does not have trivial coding bugs and typos. Since Quint is a relatively general specification language, which stems from TLA+, it does not offer built-in primitives for modeling Solidity and EVM. Hence, to model the governance protocol, we need to create adequate reference models for the following primitives and mechanisms of the EVM smart contracts:

  • Contract inheritance,
  • Multisig,
  • Cryptographic signatures,
  • Hashing, e.g., Keccak256,
  • EVM Calls.

Modeling inheritance. In the reference implementation, two of the most important contracts from a modeling perspective are SecurityCouncil and Guardians. They inherit from Multisig and EIP712. Since Quint does not support inheritance natively, we manually emulated it by calling all necessary constructors.

For example, to create a new instance of SecurityCouncil we have to first directly create a new instance of Multisig for it:

pure def newSecurityCouncil(_members: Set[Address]): Result[SecurityCouncilState] = {
  pure val multisig = newMultisig(_members, 9)
  pure val empty = {
    multisig: multisig.v, softFreezeThreshold: 0, softFreezeNonce: 0,
    hardFreezeNonce: 0, softFreezeThresholdSettingNonce: 0, unfreezeNonce: 0
  }
  if (isOk(multisig)) {
    pure val membersSize = _members.size()
    pure val e = require(membersSize == 12,
      "SecurityCouncil requires exactly 12 members")
    if (e != "") {
      err(empty, e)
    } else {
      ...
    }
  } else {
    err(empty, multisig.err)
  }
}

Modeling multisig mechanics. The ZKsync Governance Protocol is based on 2-layer multi-sig contracts: Guardians and Security Council are multi-sig contracts, and each their member (body) is also a multi-sig contract. We implemented a separate module for multi-sig that instantiates mechanics with the necessary thresholds and implemented three methods to check signatures. The implementation can be found in multisig.qnt. Notably, we have simplified the model related to ERC-1271. So, in the specification multi-sig module implements the method isValidSignatureNow which is a wrapper around the method isValidSignature.

/// @dev The function to check if the provided signatures are valid and
///      meet predefined threshold.
/// @param _digest The hash of the data being signed.
/// @param _signature An array of signers and signatures to be validated
///        ABI encoded from
///        `address[], bytes[]` to `abi.decode(data,(address[],bytes[]))`.
pure def isValidSignature(self: MultisigState, _digest: AbiEncoded,
                          _signature: Set[Signature]): Bytes4 = {
  pure val err =
    self.checkSignatures(_digest, _signature.map(s => s.signer),
                         _signature, self.EIP1271_THRESHOLD)
  if (err != "") err
  else EIP1271_MAGICVALUE
}

/// @dev Should return whether the signature provided is valid for
///      the provided data
/// @param hash      Hash of the data to be signed
/// @param signature Signature byte array associated with _data
pure def isValidSignatureNow(self: MultisigState, _digest: AbiEncoded,
                             _signature: Set[Signature]): bool = {
  isValidSignature(self, _digest, _signature) == EIP1271_MAGICVALUE
}

Modeling signing and hashing. As is typical for smart contracts in Solidity, the ZKsync governance contracts are extensively using the hash function keccak256 to compute message digests. In particular, these digests are used in the EIP-721 signature verification (see above). In addition to that, the contracts also call abi.encode and abi.decode to pack and unpack data structures into/from arrays of bytes, respectively. If we were to specify the behavior of these functions directly, we would have to implement plenty of arithmetic computations in Quint. As we use symbolic execution and satisfiability-modulo-theory solvers to analyze the protocol specification, we have to avoid heavy arithmetic computations. It is well-known that SMT solvers are slowing down on complex arithmetic constraints very quickly. Hence, we have to avoid the actual cryptographic implementations of hashing, be it the actual implementations or simplified ones. Fortunately, we can draw inspiration from classic security research such as the Dolev-Yao model.

In Dolev-Yao, encryption and decryption functions encrypt and decrypt are symbolic and uninterpreted in the sense that the main property of these functions is as follows: decrypt(encrypt(M)) = M, for an arbitrary message M. In a similar spirit, we could treat a hash function symbolically, that is, require that hash(M1) = hash(M2) if and only if M1 = M2. This is a cool idea: We don’t have to explain to the solver how real-life cryptography works but rely on a few simple axioms.

One issue that stops us from naively implementing Dolev-Yao in Quint is the Quint’s type system. First, Quint does not support uninterpreted functions. Second, even if it did, we would have to deal with the fact that the messages have plenty of different types. Interestingly, this would not be an issue in an untyped specification language such as TLA+. Fortunately, we do not have to specify the behavior of hashing for arbitrary messages. We only have to do it for the kinds of messages that are mentioned in the ZKsync contracts. Luckily, there are not so many of them. As a result, we define the shape of the hashable messages with AbiElem and AbiEncoded:

type AbiElem =
  AbiStr(str) | AbiInt(int) |
  AbiUpgradeProposal(UpgradeProposal) | AbiL2Proposal(L2GovernorProposal)
type AbiEncoded = List[AbiElem]

Further, we define several versions of abi.encode for a different numbers of arguments, and keccak256 simply as the identity function over AbiEncoded:

pure def abi_encode1(e1: AbiElem): AbiEncoded = [e1]
pure def abi_encode2(e1: AbiElem, e2: AbiElem): AbiEncoded = [e1, e2]
pure def keccak256(enc: AbiEncoded): AbiEncoded = enc

Consider the following Solidity expression:

_hashTypedDataV4(keccak256(
  abi.encode(APPROVE_UPGRADE_SECURITY_COUNCIL_TYPEHASH, _id)
))

We specify the above expression as:

[ AbiStr("SecurityCouncil"), AbiInt("1"), _id ]

Modeling the history of EVM Calls. One of our goals when writing the Quint specification is to enable effective reasoning about the protocol properties. Many expected properties of ZKsync governance require us to reason about the calls made when processing a specific external method. To enable reasoning about calls, we introduce the history of calls that are explicitly included in the EVM state:

type EvmState = {
  blockTimestamp: Uint256,
  …
  // the history of calls made in the last transaction
  ghostCallHistory: EvmCallHistory,
}

type EvmCallHistory = {
  lastSender: Address,
  calls: List[{ caller: Address, callee: Address, method: Function }]
}

This approach lets us conveniently write state invariants that reason about method calls:

val onlyGuardiansIsAllowedToCallExtendLegalVetoInv =
  evm.ghostCallHistory.calls.indices().forall(i => {
    val e = evm.ghostCallHistory.calls[i]
    and {
      e.callee == PROTOCOL_UPGRADE_HANDLER_ADDR,
      e.method == FunctionExtendLegalVeto
    } implies (e.caller == GUARDIANS_ADDR)
  })

4. Reproducing reports from Threat Modeling Submissions

In parallel with formal verification, a threat modeling exercise was conducted to identify and suggest solutions for the ZKsync governance system that may be exploited by an attacker. The development team fixed the received vulnerabilities. We, in turn, used the reported vulnerabilities to test the specification and add more invariants. For each reported vulnerability we wrote the corresponding invariant that must be violated if the vulnerability exists in the system or it must be held if the reported vulnerability was a false positive. Then we changed the specification as needed to make the system hold all invariants. For instance, consider the following report:

Emergency upgrades can be replayed infinite times on L1

Description: The EmergencyUpgradeBoard.executeEmergencyUpgrade lacks signature replay protection. So an emergency upgrade can be executed repeatedly by passing the same signatures again. This can lead to ambiguous onchain state for ZKsync protocol and can also lead to significant financial losses to users.

The ProtocolUpgradeHandler.executeEmergencyUpgrade also doesn’t prevent replaying of upgrade proposals. Even after an emergency upgrade proposal has been executed, the upgradeState function still returns UpgradeState.None as the state of that emergency upgrade proposal. Hence replay becomes possible.

We wrote the following invariant to check whether this vulnerability exists. It indirectly checks whether an emergency upgrade can be executed twice.

// An Emergency Upgrade cannot be executed twice:
// there are no two equal executed emergency upgrades.
val emergencyUpgradeMustBeExecutedOnce =
  evm.emittedEvents.indices().forall(i => {
    evm.emittedEvents.indices().forall(j => {
      match (evm.emittedEvents[i]) {
      | EventEmergencyUpgradeExecuted(id1) =>
        match (evm.emittedEvents[j]) {
        | EventEmergencyUpgradeExecuted(id2) =>
          (id1 == id2 implies i == j)
        | _ => true
        }

      | _ => true   
    }
  })
})

This invariant checks that it is not possible to make several calls to the EmergencyUpgradeHandler contract carrying the same payload, leading to a replay of the emergency upgrade.

// Emergency upgrades cannot be replayed.
//
// This invariant checks that if an external user successfully
// executes ExecuteEmergencyUpgrade call and then make the same
// call with the same arguments, the second call will return an error.
val emergencyUpgradeCannotBeReplayed = {
  val executor = EMERGENCY_UPGRADE_BOARD_ADDR
  CALLS.forall(calls => {
    SALTS.forall(salt => {
      GUARDIAN_MEMBERS.powerset().forall(guardians => {
        SECURITY_COUNCIL_MEMBERS.powerset().forall(council => {
          ZK_FOUNDATION_MEMBERS.powerset().forall(foundation => {
            val proposal = { calls: calls, executor: executor, salt: salt }
            val proposalId = keccak256_UpgradeProposal(proposal)
            val securityCouncilDigest =
              _emergencyUpgradeBoardCouncilHashTypedDataV4( 
                keccak256(abi_encode2(
                  EXECUTE_EMERGENCY_UPGRADE_SECURITY_COUNCIL_TYPEHASH, proposalId
                ))
            )
            val guardiansDigest = _emergencyUpgradeBoardCouncilHashTypedDataV4(
              keccak256(abi_encode2(
                EXECUTE_EMERGENCY_UPGRADE_GUARDIANS_TYPEHASH, proposalId
              ))
            )
            val zkFoundationDigest = _emergencyUpgradeBoardCouncilHashTypedDataV4(
              keccak256(abi_encode2(
                EXECUTE_EMERGENCY_UPGRADE_ZK_FOUNDATION_TYPEHASH, proposalId
              ))
            )
            val securityCouncilSignatures =
              signDigest(council, securityCouncilDigest)
            val guardiansSignatures = signDigest(guardians, guardiansDigest)
            val zkFoundationSignatures = signDigest(foundation, zkFoundationDigest)

            val evm2 =
              evm.externalCall(ANY_ADDRESS,
                EMERGENCY_UPGRADE_BOARD_ADDR, FunctionExecuteEmergencyUpgrade)
            val result =
              emergencyUpgradeBoard::ExecuteEmergencyUpgrade(evm2,
                calls, salt, guardiansSignatures,
                securityCouncilSignatures, zkFoundationSignatures)
                      
            isOk(result) implies {
              isErr(emergencyUpgradeBoard::ExecuteEmergencyUpgrade(result.v,
                calls, salt, guardiansSignatures,
                securityCouncilSignatures, zkFoundationSignatures))
            }
          })
        })
      })
    })
  })
}

Not all reported findings were resolved as vulnerabilities. Some were acknowledged, and the decision was to wait with fixing them immediately since there was no formal proof that the system could be transferred to an unsafe state. For instance, consider the following finding:

Signatures of governance bodies do not expire.

Description: The signatures provided by the members of Security Council and Guardian multisigs for these functions never expire:

  • Guardian.extendLegalVeto
  • Guardian.approveUpgradeGuardians
  • Guardian.proposeL2GovernorProposal
  • Guardian.cancelL2GovernorProposal
  • SecurityCouncil.approveUpgradeSecurityCouncil

Any unused signature generated for these functions can be used anytime in the future (assuming that the on-chain operation wasn’t executed).

To investigate and validate that finding for the SecurityCouncil’s approveUpgradeSecurityCouncil method, we wrote the following invariant, which was reported to hold true by the Quint simulator and the symbolic model checker.

// ApproveUpgradeSecurityCouncil call cannot be replayed.
val approveUpgradeSecurityCouncilCannotBeReplayed = {
  val IDS = getAllUpgradeIDs(evm)
  IDS.forall(id=> {
    ALL_SENDERS.forall(sender => {
      ALL_MEMBERS.powerset().forall(signers => {
        val digest = _securityCouncilHashTypedDataV4(
          keccak256(abi_encode2(APPROVE_UPGRADE_SECURITY_COUNCIL_TYPEHASH, id))
        )
        val signatures = signDigest(signers, digest)
        val evm2 =
          evm.externalCall(sender,
            SECURITY_COUNCIL_ADDR, FunctionApproveUpgradeSecurityCouncil)
        val result = securityCouncil::ApproveUpgradeSecurityCouncil(
          evm2, id, signers, signatures)
            
        isOk(result) implies {
          isErr(securityCouncil::ApproveUpgradeSecurityCouncil(
            result.v, id, signers, signatures
          ))
        }
      })
    })
  })
}

The ZKsync Governance Procedures can be considered as a structured informal English specification of how the ZKsync governance functions. Notably, the document contains temporal reasoning expressed in a legal language. For instance:

After a Soft Freeze and/or a Hard Freeze has been initiated, the Security Council may unfreeze (“Unfreeze”) the contracts at their discretion, with the approval of nine (9) Signers on the Security Multisig. Once frozen, an Emergency Upgrade may be executed in order to remove the freeze and/or initiate a subsequent freeze. An Emergency Upgrade during a freeze may include a message executed solely for the purpose of allowing the Security Council to initiate a subsequent freeze.

We have produced several invariants to capture the above paragraph. For instance, an invariant for the first statement above can be written in Quint as follows:

// After a Soft Freeze and a Hard Freeze have been initiated,
// an Emergency Upgrade must be passed before any subsequent freezes may be
// initiated.
val freezesRequireEmergencyUpgradeInv =
  def hasEmergencyUpgrade(eventIndices) = {
    eventIndices.exists(k => {
      match (evm.emittedEvents[k]) {
      | EventEmergencyUpgradeExecuted(_) => true
      | _ => false
      }
    })
  }
  evm.emittedEvents.indices().forall(i => {
    evm.emittedEvents.indices().forall(j => or {
      j <= i,
      match (evm.emittedEvents[i]) {
      | EventHardFreeze(id1) =>
        match (evm.emittedEvents[j]) {
        | EventSoftFreeze(id2) =>
            hasEmergencyUpgrade(evm.emittedEvents
              .indices().filter(k => i < k and k < j))
        | EventHardFreeze(id2) =>
            hasEmergencyUpgrade(evm.emittedEvents
              .indices().filter(k => i < k and k < j))
        | _ => true
        }
      | _ => true    
    }
  })
})

Note that we are not using temporal logic of Quint in the above property. We found that it is much easier to write down those properties as state invariants over the history of events. We store this history in the state of the EVM state machine.

6. Experimental setup

Hardware. We have been running experiments on a benchmarking server that is equipped with two AMD EPYC 7401P 24-Core Processors and 256G of RAM. This configuration allowed us to check dozens of invariants in parallel.

Techniques. To evaluate the invariants against the protocol specification, we have used three techniques that are offered by the Quint tools. These techniques are summarized in the table below.

Technique Choice of transactions Choice of data Quint command
Random simulation random random quint run
Randomized symbolic execution random symbolic quint verify --random-transitions=true
Bounded model checking symbolic symbolic quint verify

All three techniques perform stateful exploration in the execution space of the state state machine up to a given number of steps. In our case, a single step corresponds to execution of a single transaction from an externally-owned address (EOA), which are modeled as Quint actions. In a nutshell, the techniques are working as follows:

  • Random simulation picks one transaction at random at each step and then it randomly picks the transaction arguments from the predefined sets of values. For example, the simulator may randomly select the transactions SecurityCouncil::SoftFreeze, SecurityCouncil::HardFreeze, SecurityCouncil::Unfreeze. It also generates random inputs for these transactions, e.g., it generates a validity period in the range $[0, 1024]$ and it generates the sender address from the set Set(SECURITY_COUNCIL_ADDR, PROTOCOL_UPGRADE_HANDLER_ADDR, GUARDIANS_ADDR, EMERGENCY_UPGRADE_BOARD_ADDR, ANY_ADDRESS). The random simulator evaluates the invariant at every step. This technique is conceptually the same as Invariant Testing in Foundry, though it works at the protocol level instead of executing Solidity contracts.

  • Randomized symbolic execution picks a sequence of transactions at random and delegates the choice of transaction payloads to the constraint solver z3, whose goal is to break the given invariant by following the transaction sequence. For example, the symbolic executor may randomly select the transactions SecurityCouncil::SoftFreeze, SecurityCouncil::HardFreeze, SecurityCouncil::Unfreeze. Then, it evaluates the invariant for all possible payloads from the predefined sets of payloads at once.

  • Bounded model checking delegates to the constraint solver both the choice of the transaction sequence and the transaction payload. As a result, it evaluates the invariant for all possible sequences of transactions (up to $k$ transactions) and all possible payloads the predefined sets of payloads at once.

7. Experiments

As we were writing the protocol specification, we were mainly running the random simulator and randomized symbolic execution. These two techniques provided us with a fast feedback loop, when the specification had invariant violations that were relatively easy to detect. Once the specification and the invariants stabilized, we ran full scale bounded model checking experiments for $k=6$ and $k=10$. To our surprise, these experiments found five more invariant violations. All of them were due to imprecision in the invariants and modeling, which we have fixed.

Individual experiments. As running all experiments at once is time consuming, we were running experiments for individual invariants, as were were developing them. For example, the following command runs the random simulator to check the invariant emergencyUpgradeUnfreezesStateInv against 10,000 randomly generated sequences of transactions, each sequence having up to 10 transactions:

$ quint run --max-steps=10 --max-runs=10000 \
  --invariant=emergencyUpgradeUnfreezesStateInv main.qnt
...
[ok] No violation found (327024ms).
Use --seed=0x14360563a7e48f to reproduce.

Similarly, the following command runs randomized symbolic execution to check the invariant emergencyUpgradeUnfreezesStateInv against 100 randomly selected sequences of symbolic transactions, each sequence having up to 10 transactions:

$ quint verify --random-transitions=true --max-steps=10 \
  --invariant=emergencyUpgradeUnfreezesStateInv main.qnt
...
[ok] No violation found (750601ms).

:warning: Even though we check only 100 symbolic runs instead of 10,000 concrete runs, these 100 symbolic executions potentially cover a much larger subset of the execution space than 10,000 concrete runs.

Finally, the following command runs the bounded model checker to check the invariant emergencyUpgradeUnfreezesStateInv against all sequences of up to 5 transactions:

$ quint verify --max-steps=5 \
  --invariant=emergencyUpgradeUnfreezesStateInv main.qnt
...
[ok] No violation found (2015939ms).

:warning: Unlike random simulation and randomized symbolic execution, we ran the bounded model checker for only 5 steps in the above example, as it takes over six days to explore all executions with the bounded model checker. Higher confidence comes at the cost of longer computation times.

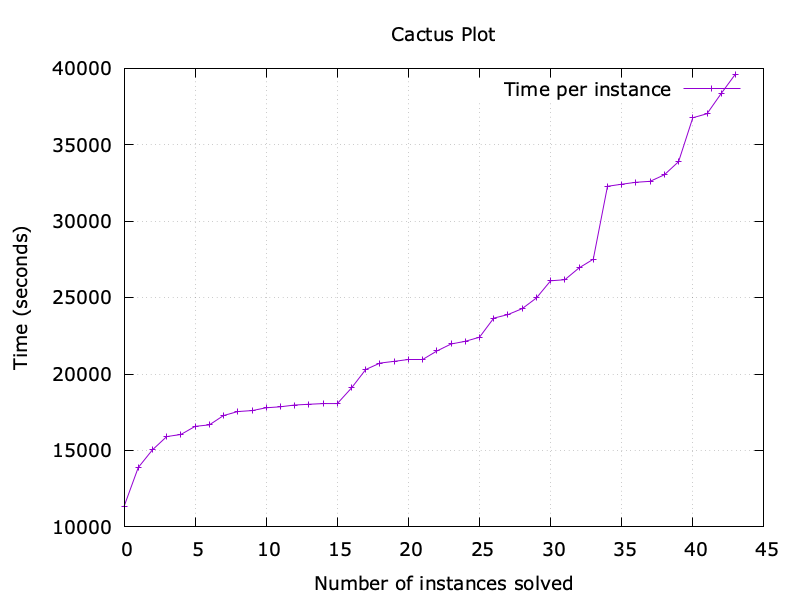
Full scale experiments. The plot below shows the time required to run the bounded model checker for all executions of up to 6 transactions, to verify the 45 invariants in parallel. The plot shows the time in seconds that was required to check each invariant, from the fastest one to the slowest one. As we can see, the fastest experiment required about 3 hours, whereas the slowest experiment required about 11 hours.

Model checking results

Degrees of confidence. As can be seen from the short overview of the Quint techniques, random simulation is the most straightforward and the fastest technique among the three. However, it provides us with the lowest degree of confidence. For instance, the probability of just choosing three specific transactions (e.g., SecurityCouncil::SoftFreeze, SecurityCouncil::HardFreeze, and SecurityCouncil::Unfreeze) out of 20 available transaction types in that order would be $\frac{1}{20^3} = \frac{1}{8000}$. If we multiply this probability by the probability of choosing the right payloads, we will see that the chance of producing a right sequence of transactions is quite low. The imprecision of this technique is compensated by the speed of executing a single transaction sequence. In our experiments, this technique has indeed missed multiple invariant violations.

Randomized symbolic execution provides us with much better guarantees. As in the case of random simulation, this technique may miss an invariant violation, when it does not generate the right sequence of transaction types, e.g., the probability of generating the sequence of three transactions is $\frac{1}{8000}$, as we discussed above. However, once the right sequence has been selected, the choice of right payloads is done by the constraint solver. As a result, this technique has much better chances of hitting invariant violations. In our experiments, this technique found multiple invariant violations, but still missed a few. Since it runs the constraint solver in the background, this technique is slower than random simulation, but it covers significantly more executions.

Bounded model checking is the most complete technique among the three. If it does not find an invariant violation for $k$ steps, it guarantees that there is no sequence of up to $k$ transactions that draws values from the set of predefined values and violates the invariant. In our experiments, this technique found five invariant violations that were missed by the other two techniques. However, it may take several days to analyze all executions, say, of up to 10 transactions.

7. Conclusions

It may seem non-obvious that we chose Quint for this task, instead of using fuzzers or formal verification tools specifically designed for Solidity. Interestingly, translating Solidity to Quint was not as much of a bottleneck in this project, as one could have expected. Most of our time went into formulating key invariants and understanding whether we had specified sufficiently many invariants.

In general, we had a very fast feedback loop from writing an invariant to finding a counterexample, if there was one. In addition to that, we used both the randomized simulator of Quint, which is conceptually close to the fuzzer in Foundry. After running the randomized simulator, to increase our confidence, we were running the symbolic model checker Apalache, which is closer to symbolic execution tools that are backed by SMT solvers. This required literally zero boilerplate code, as the Quint tools are built on the concept of state machines, invariants, and the temporal logic of TLA+.