This is Part 3 of a three-part blog post. If you have not read Part 1 and Part 2, please do that first.

3. Testing and Checking the Properties

Now it is time to check our properties! We will use two Quint commands:

  • quint run that runs the randomized simulator,
  • quint verify that runs the model checker Apalache.

If you wish to reproduce the experiments, use the specification prng2.qnt.

3.1. Testing the Properties with the Simulator

To test both properties, we simply use quint run:

$ quint run --invariant=safety ./specs/prng2.qnt
An example execution:

[State 0] { base: 1, bound: 3724719, input: 3724719, output: 0, pc: InLoop }
[State 1] { base: 256, bound: 3724719, input: 14549, output: 110, pc: InLoop }
[State 2] { base: 65536, bound: 3724719, input: 56, output: 28236, pc: InLoop }
[State 3] { base: 65536, bound: 3724719, input: 56, output: 618060, pc: Done }

[ok] No violation found (1248ms).

$ quint run --invariant=missingOutput ./specs/prng2.qnt
An example execution:

[State 0] { base: 1, bound: 7132656, input: 7132656, output: 0, pc: InLoop }
[State 1] { base: 256, bound: 7132656, input: 27861, output: 46, pc: InLoop }
[State 2] { base: 65536, bound: 7132656, input: 108, output: 11795, pc: InLoop }
[State 3] { base: 65536, bound: 7132656, input: 108, output: 2895379, pc: Done }

[ok] No violation found (1288ms).

In both cases, the simulator has exercised 10,000 random executions. This is the default setting that we can change by setting --max=samples e.g. to 1,000,000.

:raising_hand: Does it mean that both properties hold true? Not exactly. Similar to property-based testing, the simulator reports a property violation, if it finds one. However, if the simulator does not find a bug, all we know is that the executions tried by the simulator, e.g., 1,000,000 executions, do not violate the invariants.

Of course, we can always increase the number of executions. We have to be aware though that the simulation times are increasing linearly with the number of executions. See the plot for the both invariants below.

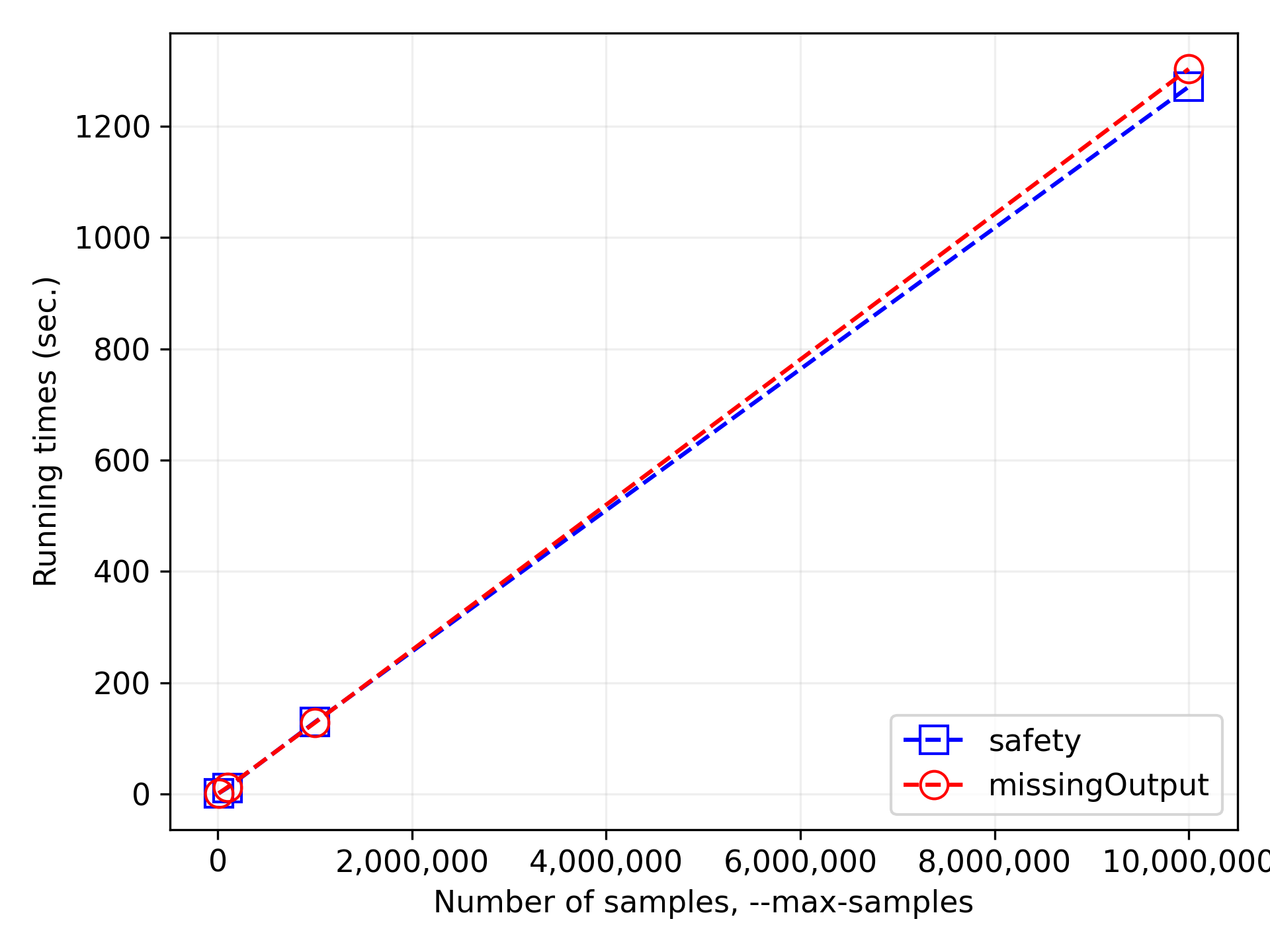
:raising_hand: How many executions shall we enumerate, to be completely sure that the invariant missingOutput holds true? Since we have fixed $bound$ to 0xff0001, we know the following:

  • Action init produces one state under the assumption that $bound$ equals to 0xff0001.

  • Action loop is executed exactly two times. Each time, this action non-deterministically chooses a value in the interval $[0, \texttt{WORD_BOUND})$.

  • Action postLoop is executed once. It non-deterministically chooses a value in the interval $[0, \texttt{WORD_BOUND})$.

Hence, for $bound = \texttt{0xff0001}$, we have $\texttt{WORD_BOUND}^3$ executions. Under the assumption of $\texttt{WORD_BOUND}=2^8$, we have $2^{24}$ executions! This is about 17 million executions. According to our plot, enumerating all these executions would take about 1 hour, even though we would have to distinguish visited executions from unvisited executions somehow. In case of $\texttt{WORD_BOUND}=2^{32}$, we would have $2^{96}$ executions. That’s really a lot!

3.2. Checking the Properties with Apalache

It would be great, if we could check the invariants against all executions at once. This is exactly what a model checker does1.

Checking Property (1). Let’s run the model checker:

$ quint verify --invariant=safety specs/prng2.qnt

An example execution:

[State 0] { base: 1, bound: 16777216, input: 16777216, output: 0, pc: InLoop }
[State 1] { base: 256, bound: 16777216, input: 65536, output: 255, pc: InLoop }
[State 2]
{ base: 65536, bound: 16777216, input: 256, output: 65535, pc: InLoop }
[State 3]
{ base: 16777216, bound: 16777216, input: 1, output: 16777215, pc: InLoop }
[State 4]
{ base: 16777216, bound: 16777216, input: 1, output: 16777215, pc: Done }

[violation] Found an issue (430ms).
error: reached a deadlock

The model checker comes back almost immediately by saying that it had found a deadlock. What does it mean? The model checker has found an execution that cannot be continued. If you look at the diagram and the example execution, it actually makes sense: We have reached a state where pc == Done. By default, the model checker does not assume that it has to deal with a terminating state machine. If we were specifying a concurrent system, then the inability to continue an execution could indicate a serious design flaw.

In our case, we expect executions to terminate. Hence, we should instruct the model checker to ignore deadlocks. The easiest way to do that is by passing a configuration file to Apalache. Below, I am using no-deadlocks.json:

$ quint verify --apalache-config=specs/no-deadlocks.json --invariant=safety specs/prng2.qnt
[ok] No violation found (170ms).

This time, the model checker tells us that it could not find a violation. Is it for real? By default Apalache checks all executions of length up to 10 steps. Since the action loop is executed up to two times (remember, that we have set MAX_NWORDS to 3), all executions contain up to four actions under our current parameters. In other words, all executions belong to one of the four shapes:

init.then(postLoop)
init.then(loop).then(postLoop)
init.then(loop).then(loop).then(postLoop)

:information_source: The above expressions are real Quint expressions, which define Runs. You can try them in REPL.

Knowing that our runs are composed of up to four actions and Apalache checks all executions up to 10 steps, we obtain a pretty solid proof that the invariant safety holds true :ballot_box_with_check:. We could even use Apalache to show that all executions are indeed having at most 4 steps under MAX_NWORDS=3, but this post is already too long.

Notice that Apalache has checked the invariant in 170ms. That was blazing fast in comparison to the simulator. On top of that, we have got much better guarantees! I was running quint verify with Apalache being bootstrapped already. If you simply run quint verify, it will bootstrap Apalache, which takes 3-4 seconds.

After running Apalache, we know that my initial hypothesis about safety being broken does not hold true. :raising_hand: Does it make the generator correct? Not yet. We still have Property (2) to check.

Checking Property (2). Recall that in Section 2.4 (Part 2) we have found out that if the invariant missingOutput holds true, then Property (2) is violated. Let’s check that with Apalache:

$ quint verify --apalache-config=specs/no-deadlocks.json \
  --invariant=missingOutput specs/prng2.qnt
[ok] No violation found (163ms).

The invariant holds true :ballot_box_with_check:. If we look at the invariant missingOutput again, what we have proved with Apalache is that whenever $bound$ is set to 0xff0001, the variable $output$ is never assigned the value 0xff0000. This definitely goes against our expectation in Property (2) :beetle:.

Again, it took Apalache 163ms to show that the invariant holds true. With the simulator, we would not be able to show that at all!

4. Root Cause Analysis

Why is it impossible to generate $output = \texttt{0xff0000}$ when $bound$ is set to 0xff0001? One way is to stare at the specification and try to find the reason. Another way is to interactively play with the specification. This is what we can do with REPL. We manually initialize the state machine with $bound$ set to 0xff0001 and replay several steps in the hope of finding the root cause:

$ quint -r specs/prng2.qnt::prng2
>>> all { bound' = 0xff0001, input' = 0xff0001, output' = 0, base' = 1, pc' = InLoop }
true
>>> step
true
>>> step
true
>>> step
true
>>> pc
Done
>>> input
255

Here we are! We cannot generate 255 (or 0xff in hex) to be the most significant word, as input == 255 and we have the following line in the specification:

  output' = (generated % input) * base + output,

If we look at the TypeScript code, this is no mistake made in translation:

  output = (squares64(state) % input) * base + output

That we take modulo input is the root cause of the problem.

We could try to quickly patch this line as follows:

  output' = (generated % (input + 1)) * base + output,

However, this would break the invariant safety, which would be easy to find with the model checker. This code needs a proper fix, which I will probably discuss in another blog post :leftwards_arrow_with_hook:.

5. Impact Analysis

Now that we know that Property (1) is satisfied, whereas Property (2) does not hold true, we have to understand the impact of Property (2) being violated. How serious is it? We have one data point, for which the PRNG never produces one output value below the bound. Once we have found the root cause of the problem, we could find more data points that confirm it.

Since the PRNG is used by the simulator, it means that the simulator never explores certain states of a state machine. As a result, for certain specifications it would never be able to reach certain states that violate a state invariant. In this context, “never” means “never”. There are no probabilities involved. This is usually called incompleteness.

As we have discussed, in contrast to the model checker, the simulator would not be able to explore all executions in practical cases. Hence, it is not a serious failure in the logic of this feature.

6. Conclusions

My first blog post happened to be so long that I broke it down into three parts. In the future, I will write shorter ones. My goal was to demonstrate you how to write specifications and use tools to quickly reason about them without going back to pen and paper, or a whiteboard. In practical terms, our specification is quite small. However, it exhibits my most favorite feature of $\tla{}$ and Quint, namely, non-determinism.

I hope you found this text entertaining. If you do, please upvote the Github discussion, leave a comment there, star the repo, etc. It is important to me to see, whether anyone is curious about this topic and I should keep writing about it. Want to chat? You can find my contact details on My webpage.

I have mentioned $\tla{}$ in this post multiple times. Showing the $\tla{}$ specification of the PRNG definitely deserves another blog post :leftwards_arrow_with_hook:.

Do you want to receive notifications when I write something new? Subscribe to the newsletter. New blog posts are going to be announced once per week (maybe twice, if I really have something!).

Powered by Buttondown.

Footnotes

  1. This statement comes with a caveat: By default Apalache checks all executions of length up to 10 steps. ↩