This is Part 2 of a three-part blog post. If you have not read Part 1, please do that first.

2. Specifying PRNG in Quint

Before we go into specification, we should ask ourselves several questions:

  1. What concern does the specification address? For example, are we more worried about the code logic being flawed, or do we really have to figure out the distribution of our PRNG?

  2. Do we want to specify the code as is, or do we want to forget some “less important” pieces?

  3. Do we want to write a specification for arbitrarily-long integers, or, say, sequences up to ten 32-bit integers would suffice?

Since my goal is to understand, whether the generator logic is flawed, or not, my answers to these questions are as follows:

  1. The specification should follow the code logic. Whether the generator’s distribution is uniform is less important to me at the moment. It is crucial though that for every integer $i$ from the interval $[0, bound)$, the probability of producing $i$ is greater than 0. Also, the generator must produce values within the bounds.

  2. We do not care about the exact behavior of square64. However, it is important to me that square64 generates all integers in the interval $[0, 2^{32})$. This means that we want to replace square64 with something more abstract. We will see how to do this below. Since the variable state only interacts with square64, we can simply drop this variable. What we are doing here is usually called an overapproximation of the behavior.

  3. It’s fine to start with the specification of big integers that could be packed into up to three 32-bit words. By having three words, we can exercise up to two loop iterations, which should be the minimal interesting case. Actually, to ease the spec debugging, I would even start with 8-bit words instead of 32-bit. What we are doing here is usually called an underapproximation of the behavior. Importantly, we should write a specification in such a way that it would be easy to generalize it.

Usually, I am writing a protocol specification in several steps: Starting with the most obvious parts and continuing with the most challenging ones. In this post, we will do it the same way.

:warning: A lot of text follows. It actually took me maybe 15-30 minutes to write a complete Quint specification and experiment with it. However, presenting and understanding the thought process requires more effort.

2.1. Specifying the Control Loop

Following $\tla{}$, Quint is built around the concept of a state machine. If I asked you to draw a state machine of the PRNG code, there is a good chance that you would draw a diagram similar to the one below:

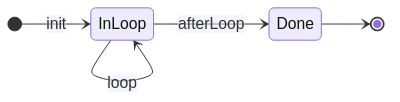
Control diagram

While this is not exactly the same state machine that $\tla{}$ experts would have imagined, this is a good starting point. Basically, we initialize the state machine, run it in a loop for a while, and, then, we are done. This is what we specify in the first version: prng1.qnt.

For the readers unfamiliar with Quint, we introduce this specification in smaller pieces that are easier to digest. The pieces to be defined later are written in <<<...>>>.

module prng1 {
  type PC = | InLoop | Done
  var pc: PC

  <<<initialisation>>>

  <<<step>>>
}

Since the PRNG code is single-threaded, we introduce one variable pc, which stands for a program counter, similar to Program counter in hardware. Quint is a typed language, so we had to declare the type associated with the variable pc, that is, the type PC. As a result, our variable pc can be assigned one of the two values: Loop or Done. If you want to learn more about the type declaration of PC, check Sum Types in the Quint language reference.

Machine Initialisation. This is how we initialize our state machine:

  action init: bool = {
    pc' = InLoop
  }

This part should be easy to understand. Once init is evaluated, the variable pc has the value InLoop, as prescribed by pc' = InLoop.

Machine Step. Similar to the the diagram, we introduce the action step, which non-deterministically chooses between two other actions: loop and postLoop.

  action step = any {
    loop,
    postLoop,
  }

  <<<actions>>>

Finally, the actions loop and postLoop are defined as follows:

  action loop: bool = all {
    pc == InLoop,
    pc' = InLoop,
  }

  action postLoop: bool = all {
    pc == InLoop,
    pc' = Done,
  }

Exercising the Machine. Our specification is not very useful, but it’s not entirely useless either. We can play with it in REPL and convince ourselves that it specifies the same behavior as shown in the diagram:

$ quint -r specs/prng1.qnt::prng1
Quint REPL 0.17.1
Type ".exit" to exit, or ".help" for more information
>>> init
true
>>> pc
InLoop
>>> loop
true
>>> loop
true
>>> postLoop
true
>>> pc
Done

Once we have played enough with this specification, let’s add the interesting part to the state machine, that is, data.

2.2. Specifying Data Transformations

Now it is time to add data to prng1.qnt. You can find a complete version of this new specification in prng2.qnt. Whereas the control part was pretty straightforward, data requires a few curious tricks.

Following the PRNG code, we simply declare four new integer variables, in addition to PC:

module prng2 {
  <<<values>>>

  type PC = | InLoop | Done
  var pc: PC
  var bound: int
  var input: int
  var output: int
  var base: int

  <<<initialisation>>>

  <<<step>>>
}

Machine Initialisation. When looking at the PRNG code, it should be fairly obvious how to initialise the variables input, output, and base. How do we initialise bound though? In the TypeScript code, bound is actually a function parameter, so it may have multiple values, and we do not have much control over which values it may receive. This sounds like a case for data non-determinism.

In principle, we could just non-deterministically pick an arbitrary integer:

  nondet generated = Nat.oneOf()
  bound' = generated

However, we would have to deal with quite large integers when debugging the specification. For the moment, I would like to work with 8-bit words and restrict bound to at most three 8-bit words. Hence, I declare two immutable values in the block <<<values>>> (called “pure values” in Quint):

  pure val WORD_BOUND: int = 2^8
  pure val MAX_NWORDS: int = 3

Once we have defined WORD_BOUND and MAX_NWORDS, we can easily write init:

  action init: bool = all {
    nondet generated = 1.to(WORD_BOUND^MAX_NWORDS).oneOf()
    all {
      bound' = generated,
      input' = generated,
    },
    output' = 0,
    base' = 1,
    pc' = InLoop,
  }

Machine Step. Now it is time to define the loop action for the loop. Most of it is straightforward, except for the call to squares64, which we omit for now:

  action loop: bool = all {
    pc == InLoop,
    input >= WORD_BOUND,
    <<<updateOutput>>>
    input' = input / WORD_BOUND,
    base' = base * WORD_BOUND,
    bound' = bound,
    pc' = InLoop,
  }

How do we update the output? Here is the line from the TypeScript code:

  output = output * U32 + squares64(state)

We know that squares64 returns a new pseudo-random value based on the value of state. The actual sequence of values produced by squares64 is not that important to us. Unless we really care about the actual distribution of values produced by squares64 (for the moment, we do not), we can replace squares64 with non-determinism:

    nondet generated = 0.to(WORD_BOUND - 1).oneOf()
    output' = output * WORD_BOUND + generated,

If you remember that the Quint simulator interprets oneOf as random choice, this looks silly: We have replaced one PRNG with another! There is a bit more to that. We will run the model checker later, and it will not have any assumptions about the value distribution. What we did here is actually an abstraction: We have replaced a very specific PRNG with logic that encompasses all PRNGs.

:information_source: What we did is somewhat similar to abstraction in programming languages. For instance, in TypeScript, we could have introduced an interface for a PRNG and declare that squares64 implements this interface. Beware! This is where the analogy ends. Interfaces in mainstream programming languages are purely syntactic. As soon as your implementation meets the syntactic requirements that is, the type signatures match, the compiler would consider your implementation to be compatible with the interface. Our abstraction is not syntactic but semantic: We have replaced a concrete PRNG with an abstract PRNG that encompasses the behavior of all possible PRNGs. To be completely precise here, I would have to prove that squares64 does indeed generate values in the interval $[0, \texttt{WORD_BOUND})$. Here I am saying that it is obvious, which is a hand-waiving argument. Perhaps, I will show how to do that in a different blog post :leftwards_arrow_with_hook:.

:warning: If you have skimmed through the last two paragraphs, I recommend you to read them again. What we have done with squares64 is pretty important, even though it was not complicated. Developing intuition about which parts of the code should remain unabstracted and which parts of the code should be abstracted is one of the most important skills in specification writing.

Having understood how to specify loop, we can easily write postLoop by following the same idea of abstraction:

  action postLoop: bool = all {
    pc == InLoop,
    input < WORD_BOUND,
    nondet generated = 0.to(WORD_BOUND - 1).oneOf()
    output' = (generated % input) * base + output,
    input' = input,
    base' = base,
    bound' = bound,
    pc' = Done,
  }

2.3. Playing with the Specification

This is an important part of specification writing. Similar to writing a program, once you have some parts of your specification working, you should run them and see what happens. Of course, we could exercise init and step in REPL. But at some point, it gets too tedious. Instead of doing that, we can also run the simulator and observe the examples it is producing:

$ quint run --max-samples=1 specs/prng2.qnt
An example execution:

[State 0] { base: 1, bound: 7098000, input: 7098000, output: 0, pc: InLoop }
[State 1] { base: 256, bound: 7098000, input: 27726, output: 181, pc: InLoop }
[State 2] { base: 65536, bound: 7098000, input: 108, output: 46427, pc: InLoop }
[State 3] { base: 65536, bound: 7098000, input: 108, output: 505179, pc: Done }

[ok] No violation found (64ms).

Since I wanted to look at the examples, I constrained the simulator to try exactly one run (by setting --max-samples=1). By running the simulator multiple times and comparing the values to what I expected, I get a bit of confidence in my specification.

Although the simulator writes that no violation was found, there was not much opportunity for the simulator to find bugs. To do something more meaningful, we have to specify the expected properties.

If I was writing a program, this is where the story would end. Perhaps, I would have written a few unit tests to make sure that the code does not break in the future. When it comes to specifications, this is the moment, when the real game starts! :video_game:

2.4. Specifying the Expected Properties

Recall that I had expressed two expected properties earlier:

  1. The generator always produces values within the bounds.

  2. For every integer $i$ from the interval $[0, bound)$, the probability of producing $i$ is greater than 0.

Property (1). This property is a state invariant: It should hold in every reachable state of our state machine. We can easily write it like follows:

  val safety = (output >= 0) and (output < bound)

We will see how to check this invariant later.

Property (2). This property is not as easy to write. To begin with, similar to $\tla{}$, Quint does not support probabilistic properties out of the box. Luckily, we only require the probability to be different from zero. Hence, we can informally rewrite Property (2) as follows:

Property (2’): (For every $bound$) for every integer $i$ from the interval $[0, bound)$, there exists a future state in which $output = i$ holds true.

The above formulation looks better. Indeed, there are no probabilities. However, there is no way to write this property in Quint either. Following $\tla{}$, Quint allows the user to specify properties of all possible behaviors. Hence, every temporal property in Quint, as well as in $\tla{}$, has an implicit universal quantifier over all executions. It is possible to specify our property in Computation Tree Logic (CTL). There are tools such as nuXmv that reason about CTL, but Quint is not one of them. Perhaps, trying nuXmv on this example is a good topic for another blog post :leftwards_arrow_with_hook:.

Is it game over :space_invader:? Not exactly. If we negate Property (2’), then we will see that we can talk about all futures again:

Property (2’’): There exists $bound$ and there exists an integer $i$ from the interval $[0, bound)$ such that for all executions, for all future states, it holds that $output \ne i$.

This looks close to $\tla{}$ and Linear Temporal Logic (see LTL), which allow us to reason about all executions. Perhaps, it would be even more obvious, if I was writing these properties in a temporal logic. However, I would maintain them in English to keep things simple (even though less precise). If you wonder how I came up with Property (2’’), I actually took a formal negation of the logic formula in $\tla{}$ :wink:.

Let us fix $bound$ to be 0xff0001 and $i$ to be 0xff0000 and write the following state invariant:

  val missingOutput = {
    (pc == Done and bound == 0xff0001) implies (output != 0xff0000)
  }

If we prove that $missingOutput$ is an invariant of our specification, then we would know that we have disproved Property (2) by providing a counterexample to this property. Here should be a cliff hanger… I am not going to keep you in suspense until the next week. This is exactly the invariant I have proved with Apalache to demonstrate that my PRNG code was flawed :beetle:.

It only remains to see how we automatically check Properties (1)-(2).

To be continued…

Continue reading in Part 3 of this blog post.

Do you want to receive notifications when I write something new? Subscribe to the newsletter. New blog posts are going to be announced once per week (maybe twice, if I really have something!).

Powered by Buttondown.