Proving consistency of two-phase commit in Lean4

Tags: specification lean distributed proofs tlaplus

In the previous blog post, we discussed specification, randomized simulation, and property-based testing of Two-phase commit in Lean 4. The obvious question is whether we can use Lean for what it was designed for, namely, proving correctness of the protocol. Yes, we can! Here is our proof plan:

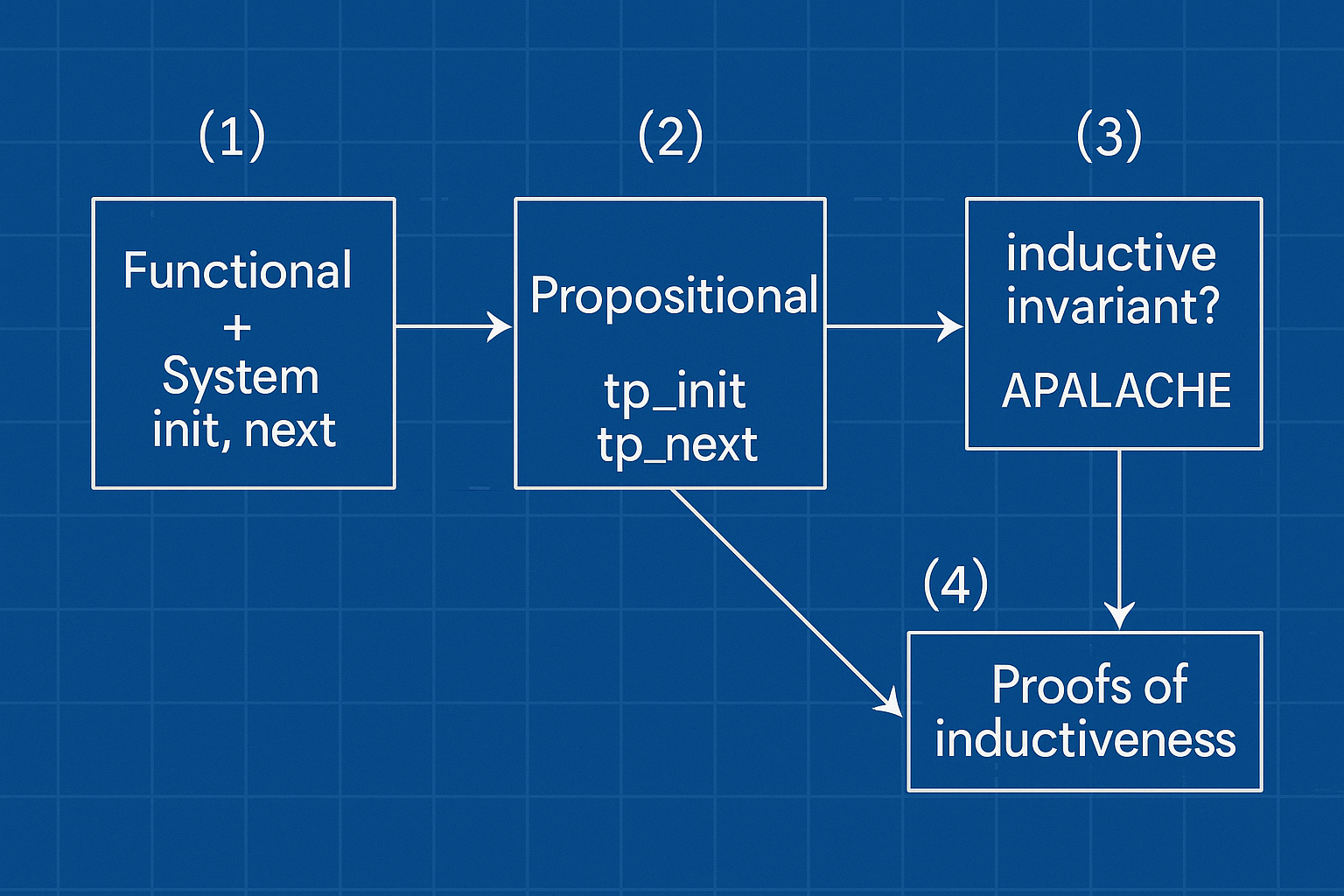
In short, I have managed to write full proofs of consistency in Lean 4, starting with a functional specification. Except for a few moments, it was clear how to proceed, though interactive proofs are tedious. In total, it took me 29 hours to write the proofs, excluding the time that was needed to read the Lean manuals. Together with specification and simulation from the previous blog post, the whole effort required 45 hours.

I believe the proofs went quickly because the inductive invariant was already correct, since we have found it with the model checker Apalache. In fact, I could probably reduce the proof times even further if I focused on minimizing the inductive invariant. If the invariant had not been correct, though, the process likely would not have gone as smoothly.

Let us have a look at the statistics in the table below.

Files	LOC (excluding comments & whitespace)
Functional.lean + System.lean	139
Propositional.lean	90
PropositionalProofs.lean	275
InductiveProofs.lean	1077

The ratio of proofs (propositional and inductive) to the system code (propositional) is about 15. This fits into the empirical ratio of software verification, where the proofs are 10-20 longer than the source code.

In this blog post, we have explored a “traditional” path of interactive theorem proving, though we have cut corners by finding the inductive invariant with the model checker.

Another route to explore is to prove equivalence between our specification in Propositional.lean and the Veil specification. The Veil examples already contain a version of two-phase commit, though it is slightly different from the two-phase commit in TLA⁺ and our specification in Lean. Perhaps, this is a good topic for another exercise.

Certainly, this is not the first exercise in using interactive theorem provers to verify safety of a distributed algorithms. To name a few examples, there were larger-scale efforts such as IronFleet, Verdi, Disel, and Bythos.

What to prove?
Connecting functional and propositional specs
Finding an inductive invariant
Proving the inductive step in Lean 4
Proving consistency with the inductive invariant
Proving the inductive base

1. What to prove?

The task does not seem simple, though. How do we approach it? Our goal is to prove the consistency of the protocol. Fortunately, we started with the specification in TLA+, so we can stand on the shoulders of giants and reuse the TLA⁺ methodology. Here is how consistency is specified in TLA⁺:

TCConsistent ==  
  (*************************************************************************)
  (* A state predicate asserting that two RMs have not arrived at          *)
  (* conflicting decisions.                                                *)
  (*************************************************************************)
  \A rm1, rm2 \in RM : ~ /\ rmState[rm1] = "aborted"
                         /\ rmState[rm2] = "committed"

This invariant looks quite similar in Lean:

def consistency (s: ProtocolState RM) : Prop :=
  ∀ rm₁ rm₂: RM,
    s.rmState[rm₁]? ≠ some RMState.Committed ∨ s.rmState[rm₂]? ≠ some RMState.Aborted

By following the TLA⁺ methodology, to show that $TCConsistent$ is an invariant of Two-phase commit, it suffices to find a state predicate $IndInv$ and prove three properties:

The initial states satisfy the invariant $IndInv$, that is, $Init \Rightarrow IndInv$.
The transition relation preserves the invariant $IndInv$, that is, $Next \land IndInv \Rightarrow IndInv’$.
The invariant $IndInv$ implies the state invariant $TCConsistent$, that is, $IndInv \Rightarrow TCConsistent$.

The invariant $\mathit{IndInv}$ is called an inductive invariant, since it allows us to reason about all states that are reachable from $\mathit{Init}$ via $\mathit{Next}$ by induction. The interesting thing is that it is sufficient to prove this principle only once and reuse it for all specifications. This is why we simply use this approach without re-proving it every time. The cool thing about Lean is that we still can re-prove this inductive principle, if we want to.

2. Connecting functional and propositional specs

Now we have to understand what to use as the initial predicate $Init$ and the transition relation $Next$. If you have read the previous blog post, you remember that we had two kinds of specifications:

A functional specification in Functional.lean and System.lean, and
A propositional specification in Propositional.lean.

Luckily, Ilya Sergey warned me that writing proofs at the functional level is hard, so I did it at the propositional level. To connect the functional spec and the propositional spec, we prove two theorems:

theorem tp_init_correct (all: List RM) (s: ProtocolState RM):
    tp_init all s ↔ init all = s := by

theorem tp_next_correct (s: ProtocolState RM) (s': ProtocolState RM):
    tp_next s s' ↔ ∃ a: Action, next s a = some s' := by

You can find complete proofs in PropositionalProofs.lean. What’s interesting, it took me just 2.5 hours to write the equivalence proofs for all seven actions. That was fast, because once I wrote three proofs, the remaining four were completely generated by Copilot! As I expected, these proofs were relatively easy to write.

For instance, here is the function tm_commit in the functional specification:

/--
  The transaction manager commits the transaction. Enabled iff the TM is its initial
  state and every RM has sent a `Prepared` message.
 -/
def tmCommit :=
    if s.tmState = TMState.Init && s.tmPrepared = s.all then some {
        s with
        tmState := TMState.Committed,
        msgs := s.msgs ∪ { Message.Commit }
    } else none

And here is the propositional version tm_commit, which looks very much like an action in TLA⁺:

/-- The proposition version of `tmCommit`. -/
def tm_commit: Prop :=
    s.tmState = TMState.Init
  ∧ s.tmPrepared = s.all
  ∧ s'.tmState = TMState.Committed
  ∧ s'.msgs = s.msgs ∪ { Message.Commit }
  ∧ s'.tmPrepared = s.tmPrepared
  ∧ s'.rmState = s.rmState
  ∧ s'.all = s.all

The theorem tm_commit_correct is connecting both of them.

theorem tm_commit_correct (s: ProtocolState RM) (s': ProtocolState RM):
    tm_commit s s' ↔ tmCommit RM s = some s' := by
  apply Iff.intro
  case mp =>
    intro hrel
    simp [tm_commit] at hrel
    rcases hrel with ⟨ h_tmState, h_tmPrepared, h_tmState', h_msgs',
      h_tmPrepared', h_rmState', h_all' ⟩
    simp [tmCommit, h_tmState, h_tmPrepared]
    apply ProtocolState.ext
    repeat simp [*]

  case mpr =>
    intro heq
    simp [tmCommit] at heq
    rcases heq with ⟨ ⟨ h_tmState, h_tmPrepared ⟩, h_seq ⟩
    unfold tm_commit
    simp [h_tmState, h_tmPrepared]
    cases h_seq
    repeat simp [*]

If you are like me, it is hard to make sense of this proof by just starring at it, in contrast to pen & paper proofs. If you want to understand the proof, download the spec and go over the proof line by line with the Lean plugin. Of course, you would have to understand how the proofs are organized in Lean. The book on Theorem Proving in Lean 4 explains this.

It took me one more hour to prove the theorem tp_next_correct. However, when I turned to tp_init_correct, I got carried away trying to prove a statement that was too difficult. The proof involved several inductive arguments about hash maps, and I ended up spending four hours wrestling with a challenging fact. Once I clarified that, it only took 30 minutes to write a simpler and more effective proof.

Basically, the entire set of refinement proofs could be completed in a single day! The fact that Copilot was able to fill in four out of seven cases suggests that these proofs could be generalized into a broader lemma. This is evident from the structure of the proofs. I decided to leave them as they are for now, but we should consider making them more compact for easier maintenance.

For the remainder of this post, we will use only the propositional specification.

3. Finding an inductive invariant

To follow the proof methodology, we have to find $IndInv$. We could try to use our goal invariant consistency as a candidate for the invariant. However, safety properties rarely work as inductive invariants. Intuitively, an inductive invariant should generalize all reachable states, and consistency is too weak for that role.

How do we find $IndInv$? One approach would be to start with True, then try to prove the three properties. Once we understood why True is not good enough, add constraints. Repeat. In theory, this approach could work. In practice, it is too hard, as we have to write proofs by hand. It may happen that we finish 90% of a proof just to find that our candidate for $IndInv$ was not good enough.

We do not have to go the hard way. Instead, we can just use a model checker for TLA⁺ to quickly iterate on a candidate for an inductive invariant for a small set of resource managers. This is exactly what we did for our paper at OOPSLA19 at some point in 2018. I guess, it should be available in the artifact. In the modern version of Apalache, the inductive invariant looks like this:

IndInv ==
    /\ TPTypeOK
    /\ TCConsistent 
    /\ (\E rm \in RM: rmState[rm] = "committed") => tmState = "committed"
    /\ tmState = "committed" => /\ tmPrepared = RM
                                /\ \A rm \in RM: rmState[rm] \notin {"working", "aborted"}
                                /\ MkCommit \in msgs
    /\ tmState = "aborted" => MkAbort \in msgs
    /\ \A rm \in RM:
      /\ rm \in tmPrepared =>
        /\ rmState[rm] /= "working"
        /\ MkPrepared(rm) \in msgs
      /\ rmState[rm] = "working" => MkPrepared(rm) \notin msgs
      /\ MkPrepared(rm) \in msgs => rmState[rm] /= "working" 
      /\ rmState[rm] = "aborted" =>
        \/ MkAbort \in msgs
        \/ MkPrepared(rm) \notin msgs
    /\ MkAbort \in msgs =>
        \* it is either the TM or an RM who was in the "working" state
        \/ tmState = "aborted"
        \/ \E rm \in RM:
          /\ rmState[rm] = "aborted"
          /\ rm \notin tmPrepared
          /\ MkPrepared(rm) \notin msgs                 
    /\ MkCommit \in msgs =>
        /\ tmPrepared = RM
        /\ \/ tmState = "committed"
           \/ \E rm \in RM: rmState[rm] = "committed"

By running Apalache, we can make sure that our invariant is inductive for three resource managers:

$ apalache-mc check --length=0  --init=Init --inv=IndInv MC3_TwoPhaseTypedInv.tla
...
Total time: 1.282 sec
$ apalache-mc check --length=1 --init=IndInv --inv=IndInv MC3_TwoPhaseTypedInv.tla
...
The outcome is: NoError
Total time: 1.621 sec
$ apalache-mc check --length=0  --init=IndInv --inv=TCConsistent MC3_TwoPhaseTypedInv.tla
...
The outcome is: NoError
Total time: 1.342 sec

We can do the same for 7, 20, and even 50 resource managers. However, as we increase the number of resource managers, the model checker takes longer to verify the properties. For example, checking inductiveness for 20 resource managers takes about 8 seconds, compared to just 2 seconds for 3 resource managers.

To make sure that the model checker is not just printing "NoError" but also doing something useful, we replace "committed" with "aborted" in the last line of IndInv. In this case, the model checker immediately gives us a counterexample to induction.

$ apalache-mc check --length=1 --inv=IndInv --init=IndInv MC3_TwoPhaseTypedInv.tla
...
Check the trace in: [...]/violation1.tla
State 1: state invariant 5 violated.
Total time: 1.760 sec

Basically, this is how we speed up the guess-work of finding an inductive invariant with the model checker.

Interestingly, we can remove the line /\ TCConsistent, and Apalache does not complain. This constraint is redundant. It is actually great that we have removed this redundant constraint, as it would take us much longer to write interactive proofs with this constraint in place.

We IndInv as a conjunction of six lemmas in Lean, as it is easier to reason about the invariant this way:

-- Our inductive invariant that we use to prove the consistency property.
def invariant (s: ProtocolState RM) : Prop :=
  lemma1 s ∧ lemma2 s ∧ lemma3 s ∧ lemma4 s ∧ lemma5 s ∧ lemma6 s

You can find all six lemmas in InductiveProofs.lean. For example, here is how we write lemma1:

def lemma1 (s: ProtocolState RM): Prop :=
  (∃ rm: RM, s.rmState[rm]? = some RMState.Committed) → s.tmState = TMState.Committed

If you look carefully at lemma5 and lemma6 in InductiveProofs.lean, you will notice that they also have redundancies. I missed that and this resulted in a lot of extra work when writing proofs. It would only take several seconds to check with Apalache, whether we could remove these subformulas. More on that later.

4. Proving the inductive step in Lean 4

Now that we know our invariant is inductive for small sets of resource managers, we have good chances of proving the inductive step of invariant. The transition relation tp_next is a disjunction of seven smaller subformulas such as tm_commit and tm_abort. Further, invariant is a conjunction of six lemmas.

Thus, our plan is very simple: Prove inductiveness for each of the seven actions and each of the six lemmas. This gives us 42 facts to prove. While this sounds like a lot of work, the good news is that proving 42 smaller lemmas is easier than proving one huge theorem.

Actually, the above decomposition is not hand-waiving. Our theorem invariant_is_inductive is proven exactly by this decomposition. Below you can see the first six cases:

/--
 Showing that `invariant` is inductive, that is, it is preserved by the transition relation.
-/
theorem invariant_is_inductive (s: ProtocolState RM) (s': ProtocolState RM)
  (h_all: ∀ rm: RM, rm ∈ s.all) (h_inv: invariant s) (h_next: tp_next s s'):
    invariant s' := by
  unfold tp_next at h_next
  cases h_next
  case inl h_tm_commit =>
    -- action tm_commit
    unfold invariant
    -- prove the lemmas one by one
    apply And.intro
    . exact invariant_is_inductive_tm_commit_lemma1 s s' h_tm_commit
    . apply And.intro
      . exact invariant_is_inductive_tm_commit_lemma2 s s' h_all h_inv h_tm_commit
      . apply And.intro
        . apply invariant_is_inductive_tm_commit_lemma3 s s' h_tm_commit
        . apply And.intro
          . exact invariant_is_inductive_tm_commit_lemma4 s s' h_inv h_tm_commit
          . apply And.intro
            . exact invariant_is_inductive_tm_commit_lemma5 s s' h_inv h_tm_commit
            . exact invariant_is_inductive_tm_commit_lemma6 s s' h_tm_commit

  case inr h_rest =>

(If you know how to write the above decomposition nicer in Lean, please leave a comment below.)

Now we have to prove 42 lemmas by writing the proofs. For example, here is the proof for the action tm_commit and lemma1:

-- Effort: 10m
lemma invariant_is_inductive_tm_commit_lemma1 (s: ProtocolState RM) (s': ProtocolState RM)
  (h_tm_commit: tm_commit s s'):
    lemma1 s' := by
    unfold lemma1
    intro h_committed
    exact show s'.tmState = TMState.Committed by
      unfold tm_commit at h_tm_commit
      simp [h_tm_commit]

As you can see, this was an easy one. It took me just 10 minutes to write it. Actually, closer to the end of the proof, I was writing similar proofs in 1-2 minutes. You can find the remaining 41 proofs in InductiveProofs.lean. The plot below shows the total proof efforts:

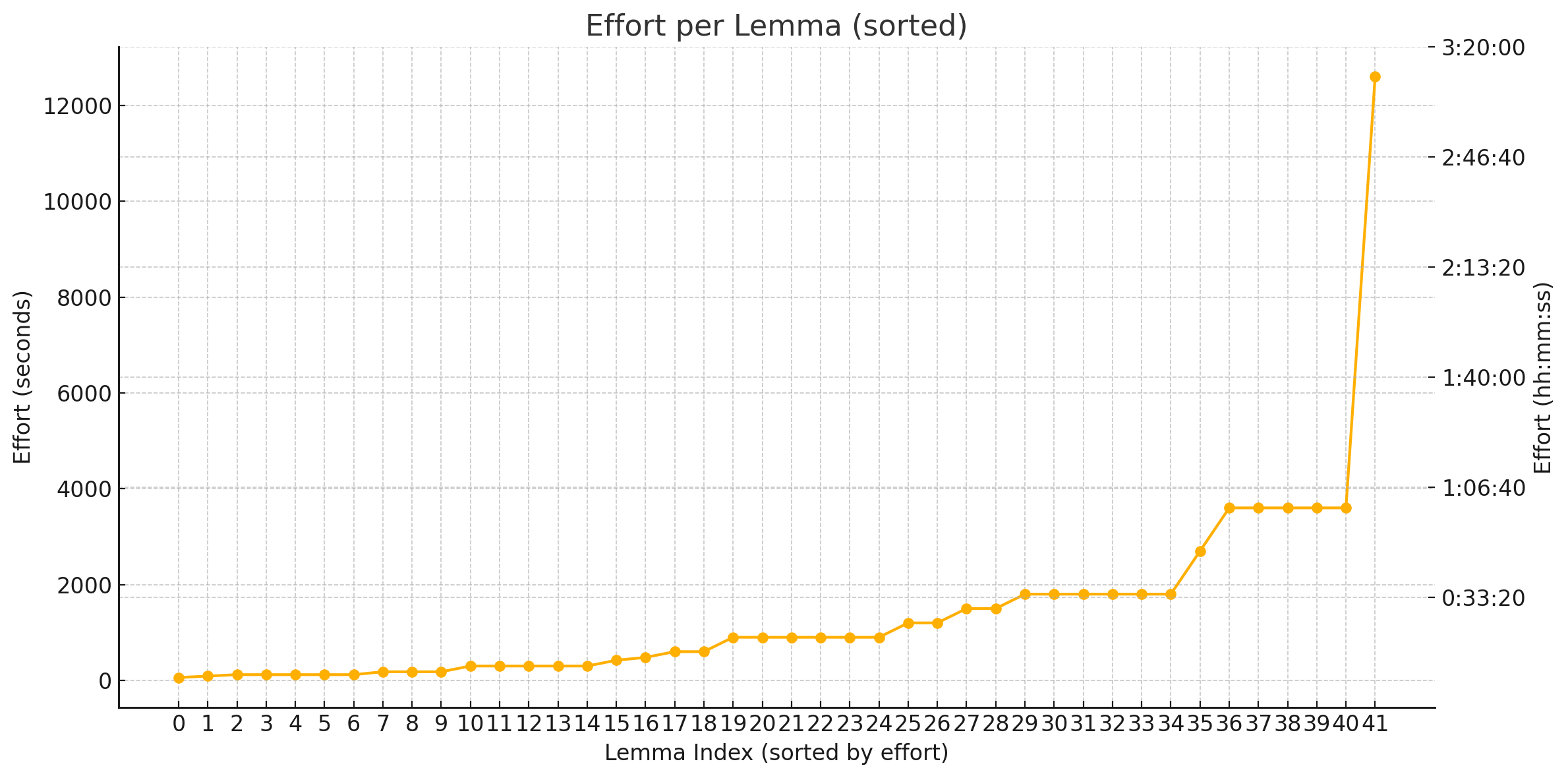
There are several things to notice:

Over a half of the lemmas took me less than 15 minutes each.
Ten lemmas took me from 20 to 30 minutes.
Six lemmas took me about 1 hour.
There is one outlier that required over three hours.

I am not exactly sure what happened with the lemma that took me so long. It was the second one I had to prove, so I might have spent a lot of time just figuring out the right tactics to use. If you look at the proof of invariant_is_inductive_tm_commit_lemma2, it involves reasoning with universal quantifiers and some small proofs by contradiction. If I were to write it again now, it probably would not take nearly as much time.

Something interesting happened when I proved about 80% of the lemmas. I got stuck. This is not really surprising, as I was at the core argument that required reasoning about one resource manager being in the Aborted state and another resource manager receiving a Commit message. Basically, I was struggling with an argument for the constraints in the commented out section below:

def lemma5 (s: ProtocolState RM) : Prop :=
  Message.Abort ∈ s.msgs → s.tmState = TMState.Aborted
  /- Added when discovering the invariant with the model checker.
      It was redundant and complicated the proof.
  (s.tmState = TMState.Aborted
    ∨ ∃ rm: RM,
        s.rmState[rm]? = some RMState.Aborted
      ∧ rm ∉ s.tmPrepared
      ∧ Message.Prepared rm ∉ s.msgs)
  -/

The commented out disjunction is not exactly wrong. The second disjunct of it implies the first disjunct. However, the second disjunct is much harder to reason about. The solution? Just remove it.

Once I have removed the redundant part, the proof was quick and easy:

lemma invariant_is_inductive_rm_rcv_commit_msg_lemma5 (s: ProtocolState RM) (s': ProtocolState RM)
  (rm: RM) (h_inv: invariant s) (h_rm_rcv_commit_msg: rm_rcv_commit_msg s s' rm): lemma5 s' := by
    unfold lemma5
    unfold rm_rcv_commit_msg at h_rm_rcv_commit_msg
    have h_unchanged_msgs: s'.msgs = s.msgs := by simp [h_rm_rcv_commit_msg]
    have h_unchanged_tm_state: s'.tmState = s.tmState := by simp [h_rm_rcv_commit_msg]
    simp [h_unchanged_tm_state, h_unchanged_msgs]
    rcases h_inv with ⟨_, _, _, _, h_lemma5_s, _⟩
    unfold lemma5 at h_lemma5_s
    exact h_lemma5_s

A similar redundancy was present in lemma6. So I removed it, too. By removing these two redundancies, I have cut the proofs in half! Small differences in proof goals may have big implications on the proof complexity.

def lemma6 (s: ProtocolState RM) : Prop :=
  Message.Commit ∈ s.msgs →
    s.tmPrepared = s.all ∧ s.tmState = TMState.Committed
    /- Added when discovering the invariant with the model checker.
        It was redundant and complicated the proof.
        (s.tmState = TMState.Committed
      ∨ ∃ rm: RM, s.rmState[rm]? = some RMState.Committed)
      -/

5. Proving consistency with the inductive invariant

Once we are sure that invariant is inductive, it is easy to prove that it implies consistency. It took me just 15 minutes to write the proof:

-- Proving that the inductive invariant implies the consistency property.
-- Effort: 15m
theorem invariant_implies_consistency (s: ProtocolState RM) (h_inv: invariant s):
    consistency s := by
  unfold consistency
  intro rm₁ rm₂
  by_contra h_committed_and_aborted -- assume the opposite
  simp at h_committed_and_aborted
  rcases h_committed_and_aborted with ⟨h_rm1_committed, h_rm2_aborted⟩
  have h_ex_committed: ∃ rm: RM, s.rmState[rm]? = some RMState.Committed := by use rm₁
  unfold invariant at h_inv
  rcases h_inv with ⟨h_lemma1_s, h_lemma2_s, _⟩
  unfold lemma1 at h_lemma1_s
  unfold lemma2 at h_lemma2_s
  have h_tm_committed: s.tmState = TMState.Committed := by exact h_lemma1_s h_ex_committed
  simp [h_tm_committed] at h_lemma2_s
  rcases h_lemma2_s with ⟨_, _, h_no_working_or_aborted⟩
  specialize h_no_working_or_aborted rm₂
  rcases h_no_working_or_aborted with ⟨_, h_rm2_not_aborted⟩
  rw [h_rm2_aborted] at h_rm2_not_aborted
  exact h_rm2_not_aborted rfl

6. Proving the inductive base

Finally, we have to show that the initial states also satisfy invariant. Here is just the header of the theorem:

theorem init_implies_invariant (all: List RM) (s: ProtocolState RM)
    (h_all: ∀ rm: RM, rm ∈ s.all) (h_init: tp_init all s): invariant s := by

Initially, I thought that the proof would not be harder than the proof of the inductive step, since there are fewer conditions to prove. Essentially, we have to prove six lemmas for the initial states. In total, I think it took me about three hours to finish the proofs.

This proof had an unexpected complication. I had to show that the initialization of the hash map rmState sets all resource managers to the state Working. Here is the header of this lemma:

-- show that the initialization predicate sets all the resource managers to `Working`
lemma init_rm_state_post (all: List RM) (s: ProtocolState RM)
    (h_init: tp_init all s):
    ∀ rm ∈ s.all, s.rmState.get? rm = RMState.Working := by

I observed similar issues when going through Isabelle tutorials many years ago, so I remember that sometimes one had to generalize the proof goal. This is exactly what happened here. In the end, the proof required this additional lemma:

-- An additional lemma to reason about map initialization.
-- Figuring out that we need this lemma was probably the hardest part of the proof.
lemma init_rm_keys (rm: RM):
    ∀ all: List RM,
      ∀ hashmap: Std.HashMap RM RMState,
        (all.foldl (fun m rm' => m.insert rm' RMState.Working) hashmap)[rm]? =
          if rm ∈ all then some RMState.Working else hashmap[rm]? := by

Interestingly, this is the only proof that explicitly uses the induction tactic. Even though we have been reasoning about an inductive invariant, we did not need to go into induction. Coming from TLA⁺, this is interesting. I had to use foldl to initialize the hash map, since Lean does not seem to have convenient primitives such as the function constructor. In TLA⁺, we would just use:

  [ rm ∈ RM |-> "working"]

The function constructor does not introduce explicit iteration and actually has the semantics of what I had to prove with the lemma init_rm_state_post. (To be precise, it also specifies the function domain.) Perhaps, we could introduce higher-level primitives in Lean 4 to deal with this. If you know of a better alternative to using HashMap, please let me know in the comments.