Specifying and simulating two-phase commit in Lean4

Author: Igor Konnov

Reviewers: Thomas Pani

Tags: specification lean distributed simulation pbt tlaplus

More and more people mention the Lean theorem prover in my bubble. Just the last week Ilya Sergey and co announced Veil, an IVy-like verification framework on top of Lean. Luckily, I heard a long tutorial on Lean by Sebastian Ullrich and Joachim Breitner at VSTTE24. The interesting thing about Lean is that it’s not only a theorem prover, but also a decent programming language.

So, I have decided to take on a case study of specifying a relatively simple yet interesting distributed protocol in Lean. For this reason, I did not choose a more complex consensus algorithm and instead settled on two-phase commit, for the following reasons:

• It is an interesting distributed protocol with applications in databases.

• It has been specified in TLA⁺ by Leslie Lamport, so we do not have to think about choosing the right level of abstraction. We simply follow the same level of abstraction as in the TLA⁺ specification.

It took me about three hours to translate the TLA⁺ specification into Lean spec, occasionally debating syntax and best practices with ChatGPT and Copilot along the way. See the Functional specification and System-level specification. I had to invent several patterns on the way, as specifying distributed algorithms in Lean looks like terra incognita (when compared with TLA⁺). Importantly, I tried to stay close to the original TLA⁺ specification in spirit, but not in the dogmas. My goal was to specify the protocol in a way that looks natural in Lean, instead of literally replicating the TLA⁺ idioms. In addition to that, I wanted the specification to be executable, since I was not sure about writing complete proofs of correctness. When I was writing this blog post, I realized that it is also possible to write a Propositional specification. This specification looks even closer to the original TLA⁺ specification, and also much more “natural”, if you are really into TLA⁺, even though this version is not executable.

What is intriguing is that the resulting specification had the necessary ingredients to be executable, since the Lean tools can compile a large subset of the language into C. Obviously, it does not automatically generate a distributed implementation of our distributed protocol. As we know from Quint, it is quite useful to have a randomized simulator, especially, if there are no other automatic analysis tools around.

As the next step, I wrote a very simple randomized simulator to check the properties against the specification — see Randomized simulation. It turned out to be even easier to implement in Lean than I expected. After about four hours of work, I had the simulator running and producing counterexamples to the properties that are expected to be violated. Maybe this is because I knew exactly what was needed, having written the Quint simulator a couple of years ago. Or maybe it is because Lean does not shy away from the occasional need for imperative code. Of course, this is all done through “monads”, but they are relatively easy to use in Lean — even if you are not quite ready to buy into the FP propaganda. As a bonus point, this simulator is really fast.

Of course, if you have been reading the orange website, you should tell me that writing a simulator by hand is not the way to go. Instead, we should use property-based testing (PBT). Well, after the experiments with the simulator, this is exactly what I did with Plausible. See Property-based testing. To my disappointment, PBT took took me about six hours of work, delivering less impressive results in comparison to the simulator. I wasted so much time figuring out the generators and trying to define my own instances of Sampleable and Shrinkable, that I needed something Drinkeable after that. This was a bit unexpected for me. True, it was my first time using PBT in Lean — though not my first time with PBT in general, since I had prior experience using ScalaCheck in Scala for Apalache. While PBT might be the way to go in the long run, at the moment, I find Plausible a bit too hard to use. To be fair, ScalaCheck was not trivial to figure out, too. For some reason, the PBT frameworks assume that everybody knows Haskell and QuickCheck.

After having played with the simulator and the Plausible tests, I was quite satisfied with my spec. (My experiments with more advanced language features did not lead to serious improvements in the spec.) Obviously, the next question is whether we want to prove that the protocol satisfies its state invariants. At the high-level, it is clear how to proceed: Discover an inductive invariant, prove its inductiveness and show that the inductive invariant implies the state invariants of the protocol. I must have an inductive invariant for the TLA⁺ spec of two-phase commit lying somewhere. Even if the inductive invariant is lost, I am pretty sure that it is relatively easy to find it again by iteratively running Apalache. We have seen that this is doable with Ben-Or’s Byzantine consensus. Even TLC should work for the two-phase commit. At the lower levels, it is hard to predict how much effort it would take to write complete proofs with Lean tactics. This is definitely something to do in another sprint.

To sum it up, I quite liked the experience with Lean as a programming and specification language. I will definitely add it to my set of available tools. If someone wants to write executable protocol specs in Lean, say, instead of TLA⁺, Quint, or Python, I would be happy to help.

The rest of the blogpost goes into details. If you are interested, keep reading. If not, you are free to stop here.

1. A brief intro to Two-phase commit and the TLA⁺ specification

I am giving only a very brief introduction in two-phase commit. It is quite a famous protocol. Gray & Lamport’04 (Sec. 3) explain the protocol nicely and by using the same vocabulary, as in the TLA⁺ specification. Moreover, Leslie Lamport explains the protocol idea and the specification in his Lecture 6 of the TLA⁺ Course on YouTube.

Here is the elevator pitch of two-phase commit: One transaction manager and $N$ resource managers have to agree on whether to commit or abort a transaction, e.g., a database transaction. If they all decide to commit the transaction, including the transaction manager, they all commit it. If at least one of them decides to abort, all of them should abort the transaction.

The sequence diagram below shows the happy path: Everyone decides to commit the transaction, and everybody does so:

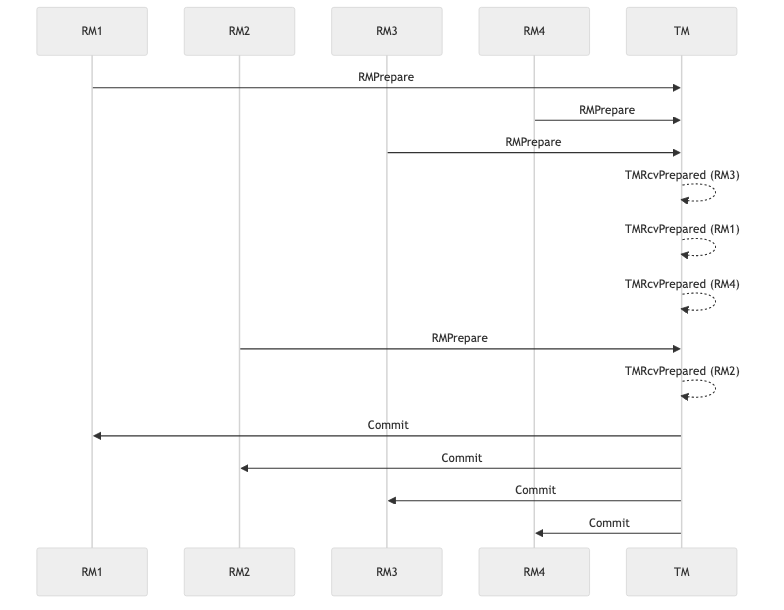
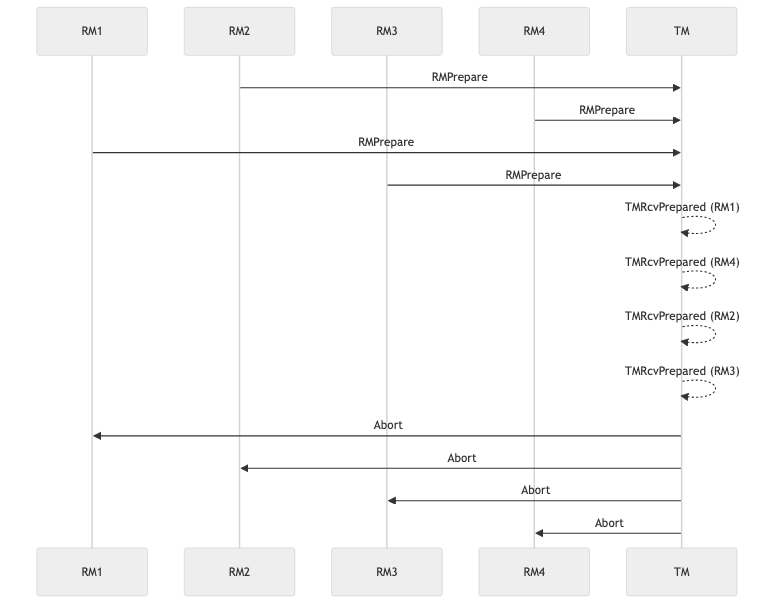
The following diagram shows an unhappy scenario, when the transaction manager declines the transaction, even though all resources managers were ready to commit:

The TLA⁺ specification. Let’s have a quick look at the TLA⁺ specification of the two-phase commit. If you don’t know TLA⁺, you can skip this part. The whole specification is about 140 lines long. As usual, it starts with the declaration of the constants and state variables:

CONSTANT RM \* The set of resource managers

VARIABLES
  rmState,       \* $rmState[rm]$ is the state of resource manager RM.
  tmState,       \* The state of the transaction manager.
  tmPrepared,    \* The set of RMs from which the TM has received $"Prepared"$
                 \* messages.
  msgs           
    (***********************************************************************)
    (* In the protocol, processes communicate with one another by sending  *)
    (* messages.  Since we are specifying only safety, a process is not    *)
    (* required to receive a message, so there is no need to model message *)
    (* loss.  (There's no difference between a process not being able to   *)
    (* receive a message because the message was lost and a process simply *)
    (* ignoring the message.)  We therefore represent message passing with *)
    (* a variable $msgs$ whose value is the set of all messages that have  *)
    (* been sent.  Messages are never removed from $msgs$.  An action      *)
    (* that, in an implementation, would be enabled by the receipt of a    *)
    (* certain message is here enabled by the existence of that message in *)
    (* $msgs$.  (Receipt of the same message twice is therefore allowed;   *)
    (* but in this particular protocol, receiving a message for the second *)
    (* time has no effect.)                                                *)

We have one specification parameter RM that fixes the set of the resource managers. Further, we have four state variables: rmState, tmState, tmPrepared, and msgs.

Since the classic TLA⁺ is untyped, the specification comes with a special predicate that captures the possible values that the state variables could have:

Message ==
  (*************************************************************************)
  (* The set of all possible messages.  Messages of type $"Prepared"$ are  *)
  (* sent from the RM indicated by the message's $rm$ field to the TM\@.   *)
  (* Messages of type $"Commit"$ and $"Abort"$ are broadcast by the TM, to *)
  (* be received by all RMs.  The set $msgs$ contains just a single copy   *)
  (* of such a message.                                                    *)
  (*************************************************************************)
  [type : {"Prepared"}, rm : RM]  \cup  [type : {"Commit", "Abort"}]
   
TPTypeOK ==  
  (*************************************************************************)
  (* The type-correctness invariant                                        *)
  (*************************************************************************)
  /\ rmState \in [RM -> {"working", "prepared", "committed", "aborted"}]
  /\ tmState \in {"init", "committed", "aborted"}
  /\ tmPrepared \subseteq RM
  /\ msgs \subseteq Message

There is also a typed version for the Apalache model checker, as it needs types. If you are interested, go and check it.

As is typical, the specification contains a series of actions, which prescribe the behavior of the resource managers and the behavior of the transaction manager. For example, RMPrepare(rm) prescribe how a resource manager rm transitions from its state "working" to the state "prepared", while sending the message [ type |-> "Prepared", rm |-> rm ]:

RMPrepare(rm) == 
  (*************************************************************************)
  (* Resource manager $rm$ prepares.                                       *)
  (*************************************************************************)
  /\ rmState[rm] = "working"
  /\ rmState' = [rmState EXCEPT ![rm] = "prepared"]
  /\ msgs' = msgs \cup {[type |-> "Prepared", rm |-> rm]}
  /\ UNCHANGED <<tmState, tmPrepared>>

The transaction manager receives that message from rm in the action TMRcvPrepared(rm):

TMRcvPrepared(rm) ==
  (*************************************************************************)
  (* The TM receives a $"Prepared"$ message from resource manager $rm$.    *)
  (*************************************************************************)
  /\ tmState = "init"
  /\ [type |-> "Prepared", rm |-> rm] \in msgs
  /\ tmPrepared' = tmPrepared \cup {rm}
  /\ UNCHANGED <<rmState, tmState, msgs>>

The individual actions such as RMPrepare(rm) and TMRcvPrepared(rm) are put together with the next-state predicate:

TPNext ==
  \/ TMCommit \/ TMAbort
  \/ \E rm \in RM : 
       TMRcvPrepared(rm) \/ RMPrepare(rm) \/ RMChooseToAbort(rm)
         \/ RMRcvCommitMsg(rm) \/ RMRcvAbortMsg(rm)

3. Specification in Lean

You can find the whole specification in Lean on GitHub. I am presenting it in small pieces, to demonstrate the decisions that had to be made.

3.1. Data structures

Let’s start with the data structures. Since Lean is typed, we have to understand how to represent the parameter RM and the state variables rmState, tmState, tmPrepared, and msgs.

When it comes to the parameter RM, which was declared with CONSTANT RM in TLA⁺, we simply declare RM to be a type variable:

-- The abstract type of resource managers.
variable (RM : Type) [DecidableEq RM] [Hashable RM] [Repr RM]

Since Lean does not make default assumptions about types, we also specify what is required from the type RM:

• RM must have decidable equality, that is, we should be able to check rm1 = rm2 for two instances rm1: RM and rm2: RM. We have [DecidableEq RM].
• RM must be usable as a key in a hash table, that is, we have [Hashable RM].
• RM must be convertible to a string, that is, we have [Repr RM].

Now we have to understand how to deal with the types of the resource manager state and the transaction manager state, which are simply written in TLA⁺ as "init", "working", "prepared", etc. To this end, we declare two types RMState and TMState, which are similar to enum types, e.g., in Rust:

/-- A state of a resource manager. -/
inductive RMState where
    | Working
    | Prepared
    | Committed
    | Aborted
    deriving DecidableEq, Repr

/-- A state of the transaction manager. -/
inductive TMState where
    | Init
    | Committed
    | Aborted
    deriving DecidableEq, Repr

Further, we should understand the type of messages, which are written in TLA⁺ like [ type |-> "Prepared", rm |-> rm ]. Again, Lean’s inductive types fit in very nicely:

/-- A message that sent by either the transaction manager or a resource manager. -/
inductive Message where
    | Commit
    | Abort
    | Prepared(rm: RM)
    deriving DecidableEq, Repr

Finally, how shall we represent the state variables rmState, tmState, tmPrepared, and msgs? To this end, we simply declare the structure ProtocolState:

/-- A state of the Two-phase commit protocol. -/
structure ProtocolState where
    -- The set of the resource managers.
    -- It may differ from run to run, but remains constant during a run.
    all: Finset RM
    rmState: Std.HashMap RM RMState
    tmState: TMState
    tmPrepared: Finset RM
    msgs: Finset (Message RM)

As you can see, ProtocolState is the place where we had to make a number of decisions:

• The state carries the set all of all resource managers. The transaction manager needs this set to decided whether it had received the messages from all resource managers, see below. Perhaps, there is some Lean magic that would do that automatically.

• rmState is a hash map from the resource managers to RMState. Recall that it was simply defined as a function in TLA⁺.

• tmPrepared is a finite set of resource managers.

• msgs is a finite set of messages.

💡 Tip:

Deciding on the field types of ProtocolState affects the rest of the specification. We could use AssocList or RBMap instead of HashMap, or HashSet instead of Finset. In the case of sets, I’ve settled on Finset, to avoid leaking the abstraction. However, in case of rmState, I found HashMap a bit more convenient. In any case, it would be good to avoid the implementation details at this level.

3.2. Functional specification in Lean

Now that we have chosen our data structures, we can specify the behavior of the two-phase commit. We do this in the module Functional.lean. For example, this is how we specify the behavior of the transaction manager on receiving the message Prepared rm, for a resource manager rm:

/-- The transaction manager receives a `Prepared` message from a resource manager `rm`. -/
def tmRcvPrepared (rm: RM) :=
    if s.tmState = TMState.Init ∧ Message.Prepared rm ∈ s.msgs then some {
        s with tmPrepared := s.tmPrepared ∪ { rm },
    } else none

The above definition is very simple, but let’s go over it, just in case:

• We check, whether the input state s (more on that below) has the field tmState set to TMState.Init.

• Further, we check, whether the set of messages contains the message Message.Prepared rm. The operator ∧ is simply “and”, whereas the operator ∈ is set membership.

• If the both of the above conditions hold true, then we produce a new state that is like the state s but its field tmPrepared is set to s.tmPrepared ∪ { rm }, that is, the set s.tmPrepared with the value rm added to it. Note that we return “some” value in this case, using the constructor some of the option type Option ProtocolState.

• If at least one of the conditions does not hold true, we return the value of type none, to indicate that the function parameter rm is not applicable in this case.

Where does the parameter s come from? It is not declared in tmRcvPrepared at all. This is an interesting feature of Lean. The parameter s is implicitly added as a parameter of tmRcvPrepared. To achieve this, we wrap the definitions in the section defs and declare s as a section variable there:

section defs
-- The state `s` is a state of the protocol, explicitly added to all the functions.
variable (s: ProtocolState RM)

def tmRcvPrepared (rm: RM) :=
  ...

def tmCommit :=
  ...

...
end defs

Here is another example of rmPrepare:

/-- Resource manager `rm` prepares. -/
def rmPrepare (rm: RM) :=
    if s.rmState.get? rm = RMState.Working then some {
        s with
        rmState := s.rmState.insert rm RMState.Prepared,
        msgs := s.msgs ∪ { Message.Prepared rm }
    } else none

Check the remaining definitions in Functional.lean.

💡 Tip:

We could translate the actions to more closely match the original specification.

If you’ve written TLA⁺ in the past, you probably expected the definition of tmRcvPrepared to look like this:

/-- The proposition version of `tmRcvPrepared`. -/
def tm_rcv_prepared (rm: RM): Prop :=
    s.tmState = TMState.Init
  ∧ Message.Prepared rm ∈ s.msgs
  ∧ s'.tmPrepared = s.tmPrepared ∪ { rm }

See the discussion about these two definitions in the Propositional specification.

💡 Tip:

If you looked at Quint, our functional definitions in Lean are quite similar to the pure def definitions of Quint.

3.3. System-level specification in Lean

Now we have the functional definitions of the resource managers and the transaction manager. How do we put these things together, to capture the behavior of the distributed system? We do this in the module System.lean.

Recall that the TLA⁺ specification does this via the predicates TPInit and TPNext:

TPInit ==   
  (*************************************************************************)
  (* The initial predicate.                                                *)
  (*************************************************************************)
  /\ rmState = [rm \in RM |-> "working"]
  /\ tmState = "init"
  /\ tmPrepared   = {}
  /\ msgs = {}

TPNext ==
  \/ TMCommit \/ TMAbort
  \/ \E rm \in RM : 
       TMRcvPrepared(rm) \/ RMPrepare(rm) \/ RMChooseToAbort(rm)
         \/ RMRcvCommitMsg(rm) \/ RMRcvAbortMsg(rm)

Initializing the system does not look hard. We do it like this:

/-- initialize the state of all resource managers to `Working` -/
def init_rm_state (all: List RM) :=
  all.foldl
    (fun m rm => m.insert rm RMState.Working)
    (Std.HashMap.emptyWithCapacity 0)

/-- The initial state of the protocol -/
def init (all: List RM): ProtocolState RM := {
    all := all.toFinset,
    rmState := init_rm_state all,
    tmState := TMState.Init,
    tmPrepared := ∅,
    msgs := ∅
}

The definition of init_rm_state definitely looks less elegant than the function constructor in TLA⁺, but it does its job: We iterate over the resource managers rm and add pairs (rm, RMState.Working) to the hash map.

What can we do about TPNext? This looks tricky: In every state, it should be possible to select one out of seven actions, as well as the parameter rm. This corresponds to control and data non-determinism, which poses a challenge to a functional definition, which is deterministic.

Luckily, the literature on distributed computing can help us with this problem. It is not unusual to define a system execution as a function of a schedule, or as a function of an adversary. Basically, we imagine that there is an external entity that tells us which steps to take.

Once we understand this trick, it becomes easy to use. We simply declare the type Action like this:

/--
Since Lean4 is not TLA+, it does not have a built-in syntax for actions.
Hence, we introduce the type that essentially turns control and data
non-deterministm into inputs. This trick is usually called a "schedule"
or "adversary" in the literature.
-/
inductive Action where
  | TMCommit
  | TMAbort
  | TMRcvPrepared(rm: RM)
  | RMPrepare(rm: RM)
  | RMChooseToAbort(rm: RM)
  | RMRcvCommitMsg(rm: RM)
  | RMRcvAbortMsg(rm: RM)
  deriving DecidableEq, Repr

Having defined the Action type, we define the function next of a protocol state s and an action a:

/-- The transition function (!) of the protocol. Since we provide `next` with
the action as an argument, `next` is a function, not a relation. -/
def next s a :=
  match a with
  | Action.TMCommit => tmCommit RM s
  | Action.TMAbort => tmAbort _ s
  | Action.TMRcvPrepared rm => tmRcvPrepared _ s rm
  | Action.RMPrepare rm => rmPrepare _ s rm
  | Action.RMChooseToAbort rm => rmChooseToAbort _ s rm
  | Action.RMRcvCommitMsg rm => rmRcvCommitMsg _ s rm
  | Action.RMRcvAbortMsg rm => rmRcvAbortMsg _ s rm

It looks simple and clean. I would argue that this definition of next is more elegant than the definition of TPNext in TLA⁺.

This is all we have in System.lean.

5. Randomised simulator in Lean

5.1. Why?

We have a formal specification in Lean. What is next? Obviously, our ultimate goal is to verify protocol correctness. In particular, we would like to verify consistency across the resource managers, for every intermediate state of the protocol:

-- the main invariant of the protocol, namely, that resource managers cannot disagree
def consistentInv (s: ProtocolState RM): Bool :=
  let existsAborted :=
    ∅ ≠ (Finset.filter (fun rm => s.rmState.get? rm = RMState.Aborted) s.all)
  let existsCommitted :=
    ∅ ≠ (Finset.filter (fun rm => s.rmState.get? rm = RMState.Committed) s.all)
  ¬existsAborted ∨ ¬existsCommitted

Basically, we want to show that it is impossible to find a protocol state, which has a resource manager in the Committed state and a resource manager in the Aborted state. Well, Lean offers us a lot of machinery for proving such properties. However, this machinery requires someone to write the proofs. Even though there is hope for large language models generating repetitive proofs, there is little hope for automatically proving properties of completely arbitrary algorithms.

Before going into a long-term effort of proving protocol properties, it is usually a good idea to try to falsify the protocol properties. This is what randomized simulations and model checkers can help us with. Even though such tools would not be able to give us a complete proof of correctness, they are quite useful in producing counterexamples. After all, if we want to prove a property $p$ and an automatic tool gives us a proof of $\neg p$, that is, a counterexample to $p$, we immediately know that the goal of proving $p$ is hopeless. Sometimes, model checkers can give us slightly better guarantees, see my recent blog post on value of model checking.

In contrast to TLA⁺, which has two model checkers TLC and Apalache, there is no model checker for Lean. Hence, the easiest approach to falsify a property in Lean is by using randomized techniques. In this section, we discuss randomized simulation. In the next section on Property-based testing, we discuss Plausible — a PBT framework for Lean.

5.2. What?

Our goal in this section is to quickly turn our Lean specification into a simulator that runs as follows:

$ lake exec RunTwophase4 100000 20 consistentInv 123

The above command runs the simulator RunTwophase4 that executes 100000 random runs, each having up to 20 steps. In each run, the simulator checks the state invariant consistentInv for each intermediate state. Since our simulator is randomized, we have to supply the seed. In our example, we give 123 as the seed. We could also supply the current time in seconds since Unix epoch by replacing 123 with $(date +%s).

Since the property consistentInv is not supposed to break, we also introduce “falsy invariants” that should actually break. By checking these invariants, we may convince ourselves that our specification is doing something useful. Here are the interesting invariants that we define right in the simulator:

-- This is a false invariant to demonstrate that TM can abort.
def noAbortEx (s: ProtocolState RM): Bool :=
  s.tmState ≠ TMState.Aborted

-- This is a false invariant to demonstrate that TM can commit.
def noCommitEx (s: ProtocolState RM): Bool :=
  s.tmState ≠ TMState.Committed

-- This is a false invariant for a trickier property:
-- Even though all resource managers are prepared, the TM can still abort.
def noAbortOnAllPreparedEx (s: ProtocolState RM): Bool :=
  s.tmState = TMState.Aborted → s.tmPrepared ≠ s.all

For example, this is how we find a schedule that makes the transaction manager commit:

$ /usr/bin/time -h lake exec RunTwophase4 1000000 20 noCommitEx 1745505753
❌ Counterexample found after 403736 trials
#0: Action.RMPrepare (RM.RM3)
#1: Action.RMPrepare (RM.RM4)
#2: Action.TMRcvPrepared (RM.RM3)
#3: Action.RMPrepare (RM.RM2)
#4: Action.TMRcvPrepared (RM.RM3)
#5: Action.TMRcvPrepared (RM.RM2)
#6: Action.TMRcvPrepared (RM.RM3)
#7: Action.RMPrepare (RM.RM1)
#8: Action.TMRcvPrepared (RM.RM4)
#9: Action.TMRcvPrepared (RM.RM1)
#10: Action.TMCommit
	2.06s real		1.88s user		0.53s sys

The simulator also finds an example, in which all resource managers were ready to commit a transaction, but the transaction manager decided to abort it:

$ /usr/bin/time -h lake exec RunTwophase4 1000000 20 noAbortOnAllPreparedEx 1745505754
❌ Counterexample found after 97860 trials
#0: Action.RMPrepare (RM.RM3)
#1: Action.RMPrepare (RM.RM4)
#2: Action.RMPrepare (RM.RM2)
#3: Action.TMRcvPrepared (RM.RM2)
#4: Action.TMRcvPrepared (RM.RM4)
#5: Action.TMRcvPrepared (RM.RM3)
#6: Action.RMPrepare (RM.RM1)
#7: Action.TMRcvPrepared (RM.RM1)
#8: Action.TMAbort
	1.21s real		0.67s user		0.32s sys

Actually, the diagrams in the Brief introduction are generated from the examples that are found by our simulator. As you can see the counterexamples are found in a few seconds, even though the simulator has to enumerate hundreds of thousands of schedules.

5.3. How?

You can find the whole simulator in Twophase4_run.lean. The core of our simulator is the following loop, written right in the entry point:

def main (args: List String): IO UInt32 := do
  -- parse the arguments
  -- ...
  -- run a loop of `maxSamples`
  for trial in [0:maxSamples] do
    let mut state := /- initial_state (...) -/ 
    -- run a loop of `maxSteps` steps
    for _ in [0:maxSteps] do
      -- ...
      let action := mkAction -- (random parameters)
      match next state action with
      | some new_state =>
        --- add to trace
      | none => -- do nothing
      -- check our invariant
      if ¬inv state then
        -- print the trace
        return 1

Before going into the details of the simulator loop, we have to introduce a bit of boilerplate code. First, we have to define the type of the resource managers RM. We do it by simply enumerating four constructors RM1, …, RM4:

-- An instance of four resource managers.
inductive RM
  | RM1
  | RM2
  | RM3
  | RM4
  deriving Repr, DecidableEq, Hashable, Inhabited

Second, since our simulator is randomized, we have to understand how to randomly produce schedules. To this end, we write the definition mkAction:

def mkAction (action_no: Nat) (rm_no: Nat): @Action RM :=
  let rm := match rm_no with
    | 0 => RM.RM1
    | 1 => RM.RM2
    | 2 => RM.RM3
    | _ => RM.RM4
  match action_no with
  | 0 => Action.TMCommit
  | 1 => Action.TMAbort
  | 2 => Action.TMRcvPrepared rm
  | 3 => Action.RMPrepare rm
  | 4 => Action.RMChooseToAbort rm
  | 5 => Action.RMRcvCommitMsg rm
  | _ => Action.RMRcvAbortMsg rm

Having defined mkAction, we simply generate two random numbers via Lean’s randNat that we supply to mkAction. Now we are ready to see the full implementation of the simulator loop:

  -- run a loop of `maxSamples`
  let mut rng := mkStdGen seed
  for trial in [0:maxSamples] do
    let mut state := init [ RM.RM1, RM.RM2, RM.RM3, RM.RM4 ]
    -- run a loop of `maxSteps` steps
    let mut trace: List (@Action RM) := []
    for _ in [0:maxSteps] do
      let (action_no, next_rng) := randNat rng 0 6
      let (rm_no, next_rng) := randNat next_rng 0 3
      rng := next_rng
      let action := mkAction action_no rm_no
      match next state action with
      | some new_state =>
        state := new_state
        trace := action::trace
      | none => pure ()

      -- check our invariant
      if ¬inv state then
        IO.println s!"❌ Counterexample found after {trial} trials"
        for (a, i) in trace.reverse.zipIdx 0 do
          IO.println s!"#{i}: {repr a}"
        return 1

As you can see, the simulator is extremely simple! There is really not much to explain here. The large body of work is done by Lean itself. Our job was to simply produce schedules, that is, lists of Action values.

5.4. Our simulator is really fast!

We have seen that in the cases when the invariant was violated — e.g., when checking noAbortEx, noCommitEx, or noAbortOnAllPreparedEx — our simulator was finding examples in a few seconds. However, we do not know the number of samples that is sufficiently large to convince ourselves that the invariant is not violated. Hence, our simulator should be fast enough to crunch plenty of runs.

Let us run the simulator on 1 million runs up to 30 steps each:

$ /usr/bin/time -h -l lake exec RunTwophase4 1000000 30 consistentInv 1745505754
	10.93s real		10.34s user		0.39s sys
           422985728  maximum resident set size
...

Nice! The simulator came back in 11 seconds and it consumed up to 434 MB of memory. We can also run it for a larger number of samples. As we can see, the simulator is quite robust. As expected, the running times are growing linearly, and there are no visible memory leaks:

Number of samples	Real Time	Max RSS (MB)
1M	10.93s	422
10M	1m43.42s	423
100M	18m7.72s	423

Is it actually fast? I think it is really damn fast! What can we use as the baseline? We can compare it with the Quint simulator. All we have to do is to get the Quint spec of two-phase commit, which is also a translation of the same TLA⁺ spec that we used as the original source. To make the comparison faithful, we have to add the instance of four resource managers like this:

module two_phase_commit_4 {
  import two_phase_commit(resourceManagers = Set("rm1", "rm2", "rm3", "rm4")).*
}

Now we can run the Quint simulator like this:

$ /usr/bin/time -l -h quint run --max-samples 1000000 --max-steps=30 \
  --invariant=consistencyInv \
  examples/classic/distributed/TwoPhaseCommit/two_phase_commit.qnt --main two_phase_commit_4
...
	27m57.62s real		28m20.04s user		21.03s sys
           217235456  maximum resident set size

This is quite interesting. Although the Quint simulator uses half as much memory, it is 168 times slower when running one million samples. I believe there are several reasons for this. First, Quint is essentially a JavaScript interpreter, while our Lean simulator is transpiled to C and compiled with full optimization for the target architecture. Second, the Quint simulator makes a slightly greater effort to find satisfying assignments randomly. Nevertheless, the performance gap is substantial.

Quint also has a new backend in Rust. Let’s try it, too:

/usr/bin/time -l -h quint run --max-samples 1000000 --max-steps=30 \
  --invariant=consistencyInv examples/classic/distributed/TwoPhaseCommit/two_phase_commit.qnt \
  --main two_phase_commit_4 --backend=rust
...
	9m27.57s real		9m24.46s user		1.53s sys
           120913920  maximum resident set size

Nice! The rust backend is three times faster and uses half as much memory as the JavaScript backend. Still, 10 minutes is nowhere close to the 10 seconds by our simulator in Lean. Apparently, it’s really hard to compete with a transpiler to C, even if the interpreter is written in

6. Property-based testing in Lean

Instead of writing our own simulator — even though it happened to be easy in the case of two-phase commit — we employ Plausible in this section. Plausible also applies randomization to check properties, but it does it in a slightly different way. Basically, it generates data structures of a given type at random up to some predefined bound and checks the property. What is interesting about property-based testing is that, once the framework finds a property violation, it tries to minimize the failing input.

You can find the whole PBT setup in Twophase4_pbt.lean and Twophase4_pbt_failing.lean. If you are using only the standard types, using Plausible looks pretty simple: Just write a quantified property, and Plausible will check it. In our case, we have two user-defined data types, namely, RM and Action. This is not unusual. In my experience, writing generators is the hardest and the most time-consuming part of using PBT. Here is how we are defining the custom type for RM and its generator:

-- An instance of three resource managers.
inductive RM
  | RM1
  | RM2
  | RM3
  | RM4
  deriving Repr, DecidableEq, Hashable, Inhabited

-- define a generator for RM
instance RM.shrinkable: Shrinkable RM where
  shrink := fun (_: RM) => []

def genRm: Gen RM := (Gen.elements [ RM.RM1, RM.RM2, RM.RM3, RM.RM4 ] (by decide))

instance : SampleableExt RM :=
  SampleableExt.mkSelfContained genRm

Basically, we define the generator genRm that randomly selects one of the four values RM1, …, RM4. Since we do not know how to further minimize a value of type RM, we simply define the instance of Shrinkable as returning the empty list.

Similar to that, we define a generator for Action RM. This time, we delegate the choice of RM values to genRm:

-- define a generator for Action RM
instance Action.shrinkable: Shrinkable (@Action RM) where
  shrink := fun (_: @Action RM) => []

def genAction: Gen (@Action RM) :=
  Gen.oneOf #[
    Gen.elements [ Action.TMCommit, Action.TMAbort] (by decide),
    (do return (Action.TMRcvPrepared (← genRm))),
    (do return (Action.RMPrepare (← genRm))),
    (do return (Action.RMChooseToAbort (← genRm))),
    (do return (Action.RMRcvCommitMsg (← genRm))),
    (do return (Action.RMRcvAbortMsg (← genRm)))
  ]
  (by decide)

instance : SampleableExt (@Action RM) :=
  SampleableExt.mkSelfContained genAction

Once we have defined the generator for actions, it is very easy to define a generator of schedules, by simply applying a standard generator in Plausible:

def genSchedule: Gen (List (@Action RM)) :=
  Gen.listOf genAction

The good news is that defining the generators was the hardest part. At least, it was the hardest part for me. Now, since Lean does not have any idea about how our specification should be executed, we define two simple functions applySchedule and checkInvariant:

-- given a concrete schedule, inductively apply the schedule and check the invariant
def applySchedule (s: ProtocolState RM) (schedule: List (@Action RM))
    (inv: ProtocolState RM → Bool): ProtocolState RM :=
  schedule.foldl (fun s a => if inv s then (next s a).getD s else s) s

-- apply a schedule to the initial state
def checkInvariant (schedule: List (@Action RM)) (inv: ProtocolState RM → Bool): Bool :=
  let init_s := init [ RM.RM1, RM.RM2, RM.RM3, RM.RM4 ]
  let last_s := applySchedule init_s schedule inv
  inv last_s

Now we are ready to write our first property to be checked by Plausible. This is how we check, whether it’s possible to reach a state where the transaction manager goes into TMState.Aborted:

-- noAbortEx
example schedule:
    let inv := fun (s: ProtocolState RM) =>
      s.tmState ≠ TMState.Aborted
    checkInvariant schedule inv
  := by plausible (config := { numInst := 3000, maxSize := 100 })

In the above definition we say that whatever the schedule we generate, checkInvariant does not return false. We configure Plausible to produce 3000 instances with the data structures bounded to 100. Comparing it to our simulator, this would mean 3000 random schedules of up to 100 steps.

In this case, Plausible finds a counterexample and minimizes it:

===================
Found a counter-example!
schedule := [Action.TMAbort]
issue: false does not hold
(1 shrinks)
-------------------

Similar to noAbortEx, we define two other properties:

-- noCommitEx
example schedule:
    let inv := fun (s: ProtocolState RM) =>
      s.tmState ≠ TMState.Committed
    checkInvariant schedule inv
  := by plausible (config := { numInst := 3000, maxSize := 100 })

-- noAbortOnAllPreparedEx
example schedule:
    let inv := fun (s: ProtocolState RM) =>
      s.tmState = TMState.Aborted → s.tmPrepared ≠ { RM.RM1, RM.RM2, RM.RM3, RM.RM4 }
    checkInvariant schedule inv
  := by plausible (config := { numInst := 3000, maxSize := 100 })

If we are lucky, both properties are violated, because they do not hold true. In my case, Plausible does not find a counterexample to noCommitEx, and it finds a counterexample to noAbortOnAllPreparedEx:

===================
Found a counter-example!
schedule := [Action.RMPrepare (RM.RM3),
 Action.RMPrepare (RM.RM4),
 Action.TMRcvPrepared (RM.RM3),
 Action.RMPrepare (RM.RM1),
 Action.RMPrepare (RM.RM2),
 Action.TMRcvPrepared (RM.RM1),
 Action.TMRcvPrepared (RM.RM4),
 Action.TMRcvPrepared (RM.RM2),
 Action.TMAbort]
issue: false does not hold
(23 shrinks)
-------------------

Finally, we define the property consistentInv, which should not be violated:

-- consistentInv
#eval Testable.check <| ∀ (schedule: List (@Action RM)),
    let inv := fun (s: ProtocolState RM) =>
      let existsAborted :=
        ∅ ≠ (Finset.filter (fun rm => s.rmState.get? rm = RMState.Aborted) s.all)
      let existsCommitted :=
        ∅ ≠ (Finset.filter (fun rm => s.rmState.get? rm = RMState.Committed) s.all)
      ¬existsAborted ∨ ¬existsCommitted
    checkInvariant schedule inv

So PBT seems to work and looks fine! The only thing that I could not figure out is how to increase the number of samples to large values, e.g., millions of samples, as we did in the simulator. Unfortunately, Plausible produces a stack overflow even on 10K examples, even when run via lake test. This needs more debugging.

7. Propositional specification in Lean

Finally, let’s discuss, whether our specification style is the most natural one when translating TLA⁺ specifications. We used the functional approach to define individual behavior of resource managers and transition managers in Functional.lean and System.lean. When we did a similar trick in Quint, some people were telling me that it’s not TLA⁺. I think it is easier to see what they meant by this in Lean!

Instead of defining functions, we can write the specification as propositions. As before, we define two variables: s for the current state, and s' for the next state.

-- The state `s` is the "current" state of the protocol.
variable (s: ProtocolState RM)
-- The state `s'` is the "next" state of the protocol.
variable (s': ProtocolState RM)

Now we can translate TLA⁺’s action TMRcvPrepared as a proposition:

/-- The proposition version of `tmRcvPrepared`. -/
def tm_rcv_prepared (rm: RM): Prop :=
    s.tmState = TMState.Init
  ∧ Message.Prepared rm ∈ s.msgs
  ∧ s'.tmPrepared = s.tmPrepared ∪ { rm }

This looks very similar to TLA⁺! Moreover, we should be able to use some definitions that do not have an executable implementation. For instance, we can use quantifiers over sets, instead of filtering sets. I also suspect that it would be easier to write proofs over such propositions rather than over functional code.

Can we find a connection between the functional definitions and the propositions? Well, in Lean we can just write simple theorems like tm_rcv_prepared_correct:

theorem tm_rcv_prepared_correct (rm: RM):
    tm_rcv_prepared s s' rm ↔
      tmRcvPrepared RM s rm = some s' := by sorry

I do not know how to write a Lean proof of the above theorem yet. In principle, it should be quite easy to write for someone proficient with Lean proofs. Indeed, the functional definition and the proposition are very close in their syntactic structure.

I find this connection especially appealing. This would let us stop arguing about which level is the right one. We could simply write both functional and propositional definitions and connect them via (hopefully!) simple proofs.